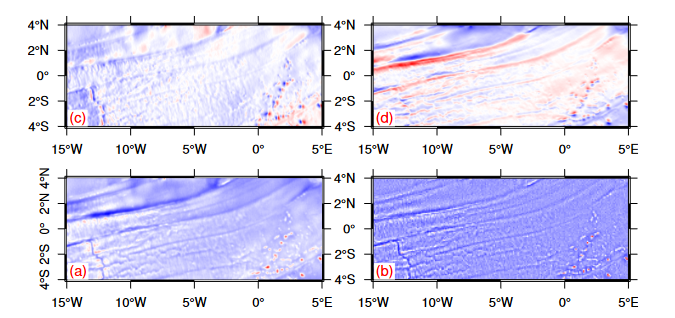
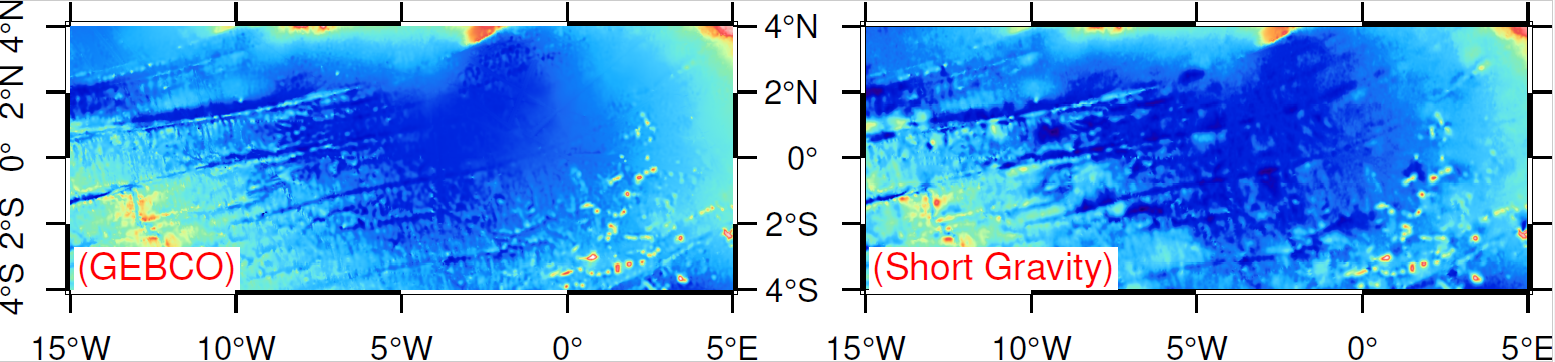
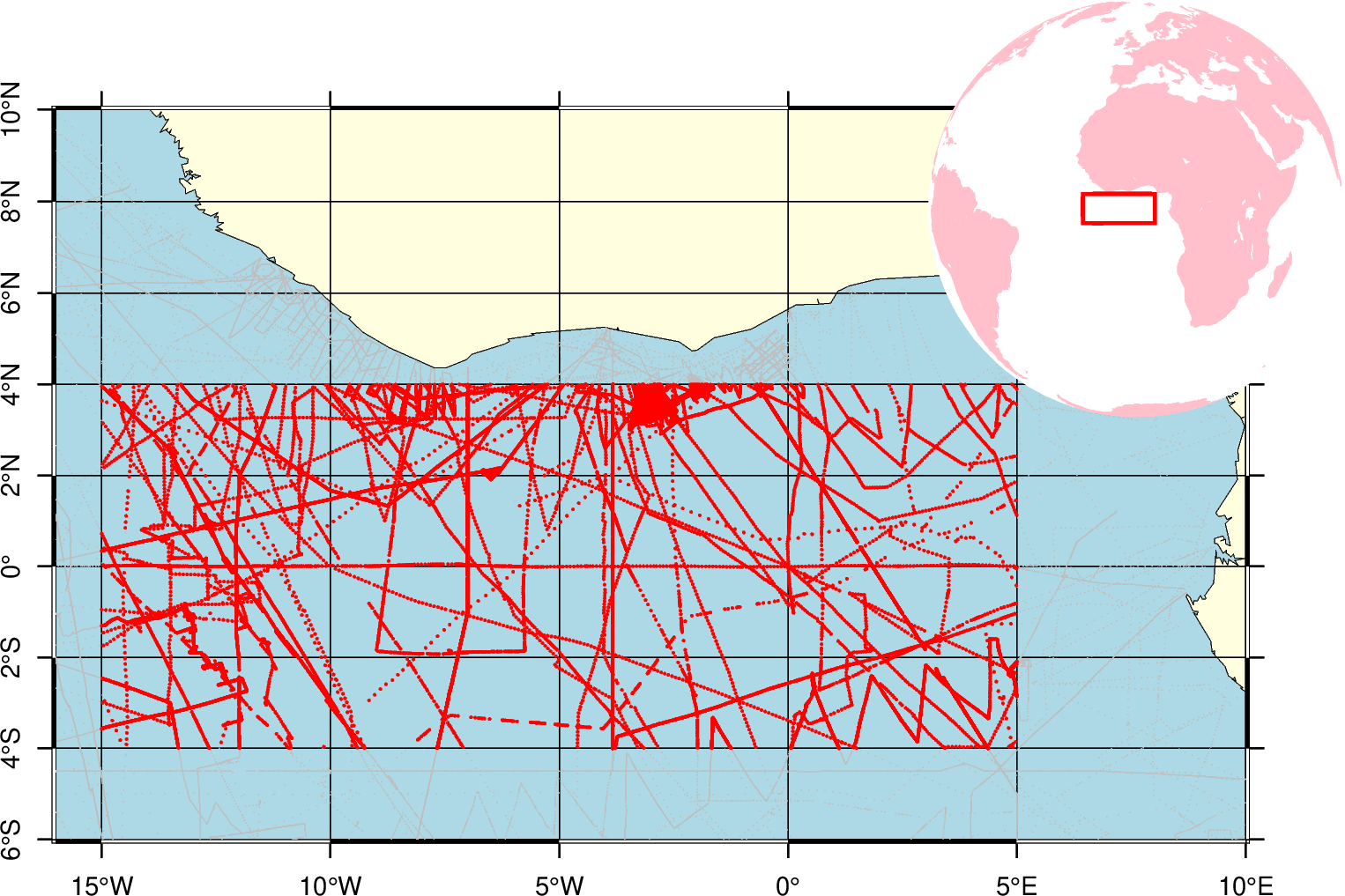
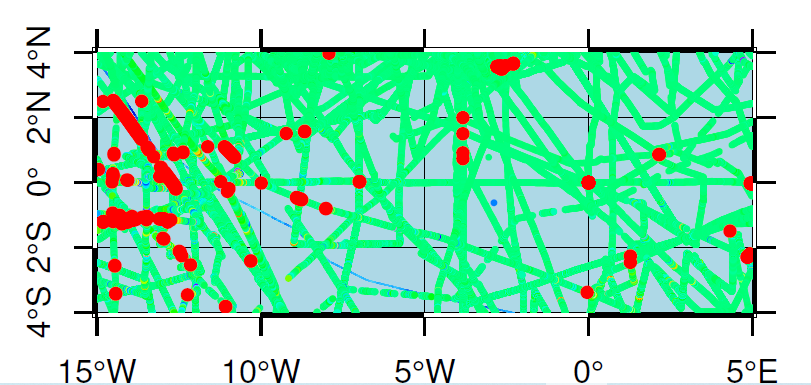
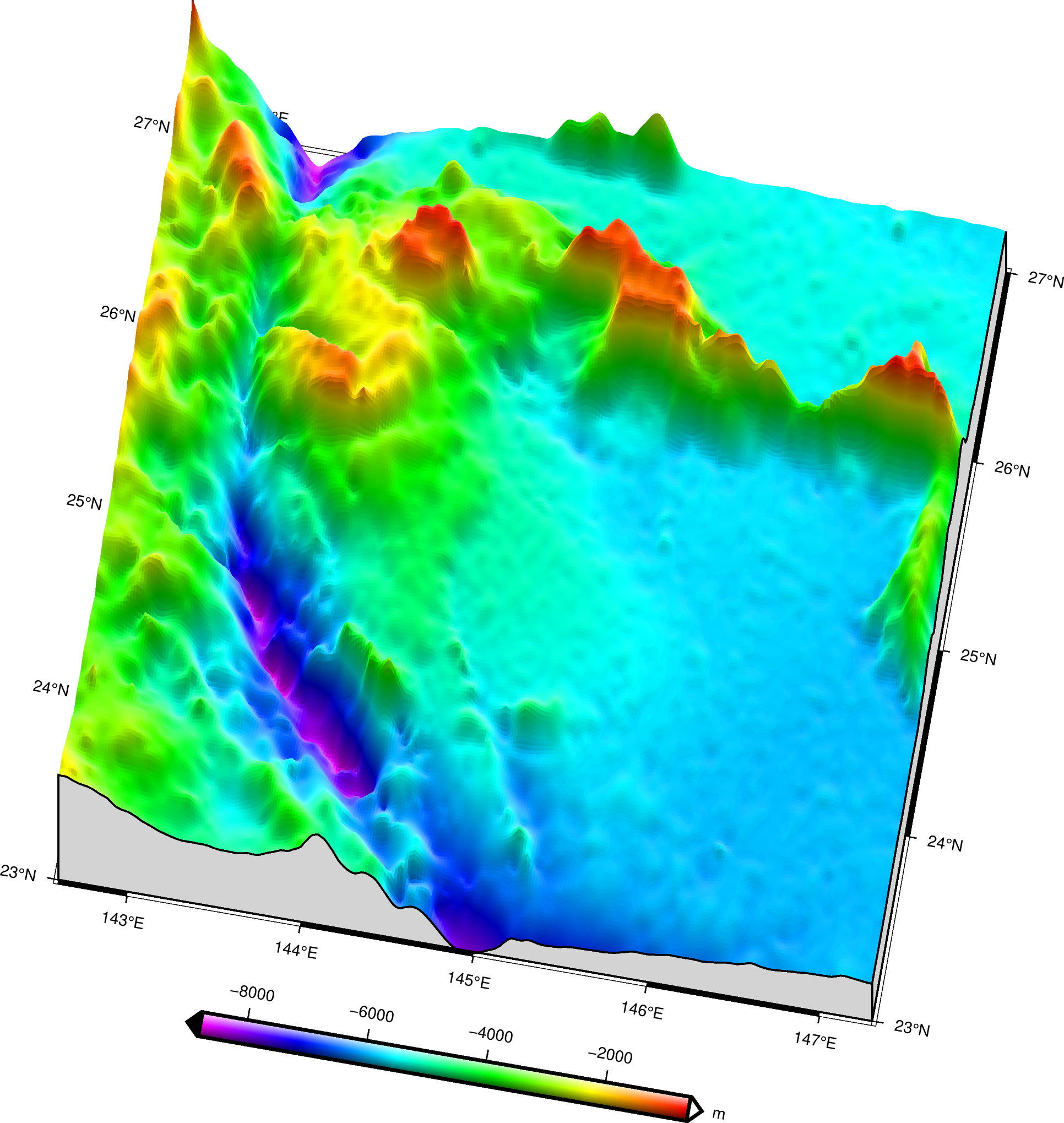
上节已备好训练数据,本节介绍CNN和DNN网络设置,跳过物理公式,直接使用备好的重力数据来预测水深,然后使用检核点水深来验证模型的精度。本节是这个AI重力水深反演系列的大结局,我们将知道以下问题的答案:
- 加入物理机制计算的短波重力能提高AI精度吗?
- 高维度的CNN是不是比低维的DNN好呢?
- 人工智能是否比传统方法效果好呢?
人工智能的海底地形反演系列在这儿暂时大结局了,但这不意味着真的结束。尽管人工智能在海洋遥感、物理海洋和其他许多地学领域取得了巨大的进展,但在大地测量、海洋测绘领域的应用可能才刚开始。其背后的原因是深刻而复杂的,这是不是测绘界的传统不无关系呢?测绘的主要工作之一就是测,也就是采集真实数据,并且非常重视数据精度和真实性这个概念,《测绘法》里面对数据真实性有明确的法律要求,篡改数据可能是犯罪行为,故对AI这种虚幻的、算出来的数据是有潜意识的否定态度;若AI精度达到多波束精度,那海洋测绘从业者可能失业,整个领域将遭遇百年未有之大变局;原因可能还有更多,欢迎私信讨论。
FC-DNN
模型构建
本例使用的深度学习框架是谷歌tensorflow,如果读者仅应用深度学习,而不研究深度学习本身,使用内置的keras包即可,因为它比较友好,上手轻松。另外,使用GPU可以提高训练速度,比如2080TI的英伟达显卡训练中,DNN每个Epoch仅3s,CNN为6s,对于本案例来说,由于数据量不大,CPU应该也不会太耗费时间。
FC-DNN即Fully-Connected (FC) Deep Neural Network (DNN),在输入和输出层的中间有一系列全连接层,本例使用的DNN网络结构如下: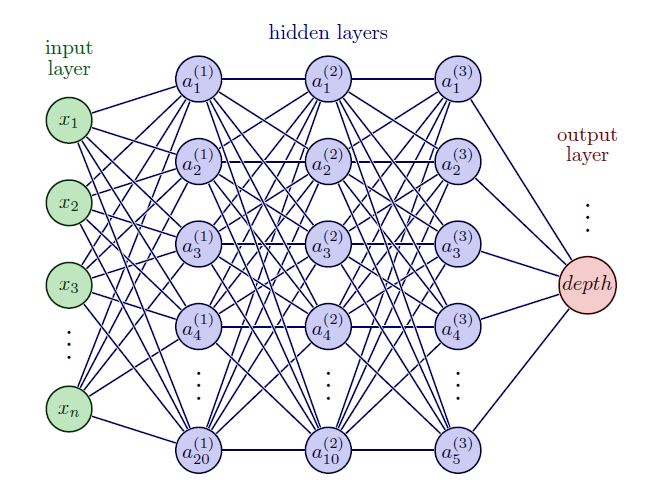
这个FC-DNN结构的中间层设计了三个全连接层,全连接顾名思义就是每个节点都互相连接,三个层的神经元数量分别是20、10、5。通过这些个连接层和神经元,经过后面的最优拟合训练,就可以构建起了重力场(input)和海底地形(output)之间的非线性关系。最终在预测水深的时候,只需要输入重力场和位置信息就可以输出对应位置的水深。
DNN结构绘图代码使用了
latex:https://github.com/GenericAltimetryTools/AIBathy/blob/main/figs/fig4/main.tex
这个FC-DNN结构对应的Python代码:
1 | model = models.Sequential() |
上面的代码中input_shape=(None,6)表示输入的元素个数,需要根据具体输入参数的类型来确定,比如如果仅仅输入经纬度和重力异常,那这儿就是3;activation='relu'表示激活函数为relu。
Keras内置的深度学习模型确实很方便,对于非计算机方向的纯用户非常好用,仅几行代码就完成了一个模型的搭建。
设置完毕后,开始训练:
1 | opt = optimizers.Adam(learning_rate=0.001) |
训练过程是确定最优拟合的过程。这里面有一些常见的设置,比如optimizer优化器、loss损失函数、epochs训练的次数等等。 这些知识点可以轻易在网上获得,因为本篇幅过长,这儿就不细说了。
网格重力到网格水深的预测
Python代码:
1 | grid_ai=model.predict(pre_case3, batch_size=120) |
通过输入网格重力pre_case3就可以直接得到归一化的网格水深,进一步还需要还原为实际水深值。
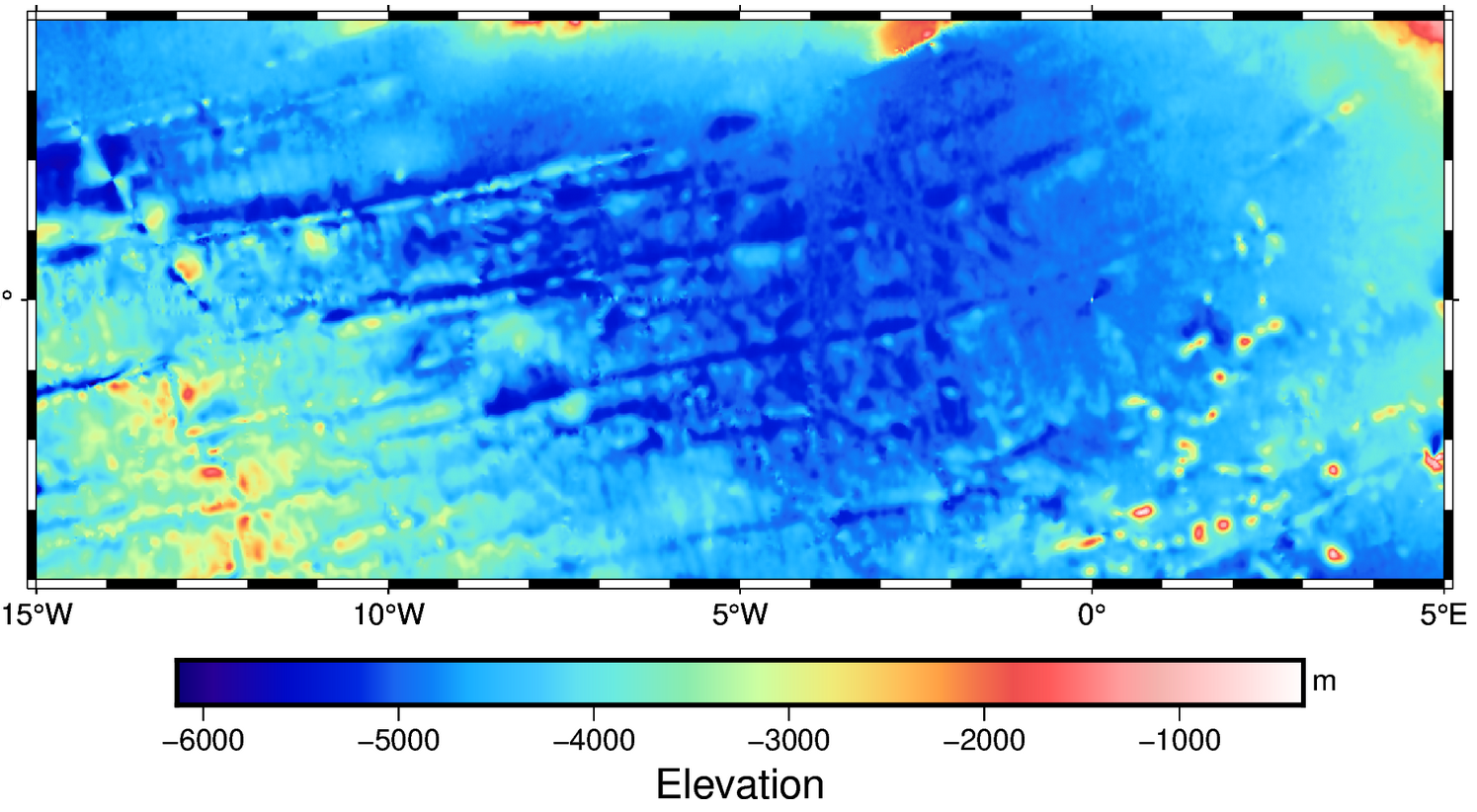
评估
1 | pre = model.predict(test_case3, batch_size=120) |
训练完成后,使用predict函数预测检核点test_case3的水深,并将归一化的预测结果还原成真实的水深,最后就可以使用实测水深对其进行统计评估了。
或者也可以使用GMT和测试数据对导出的网格进行评估,理论上效果是一样的:
1 | gmt grdtrack check_feizhou.txt -Gdepth_case1.nc | awk '{print $3,$4}' > draper.txt |
几点结果
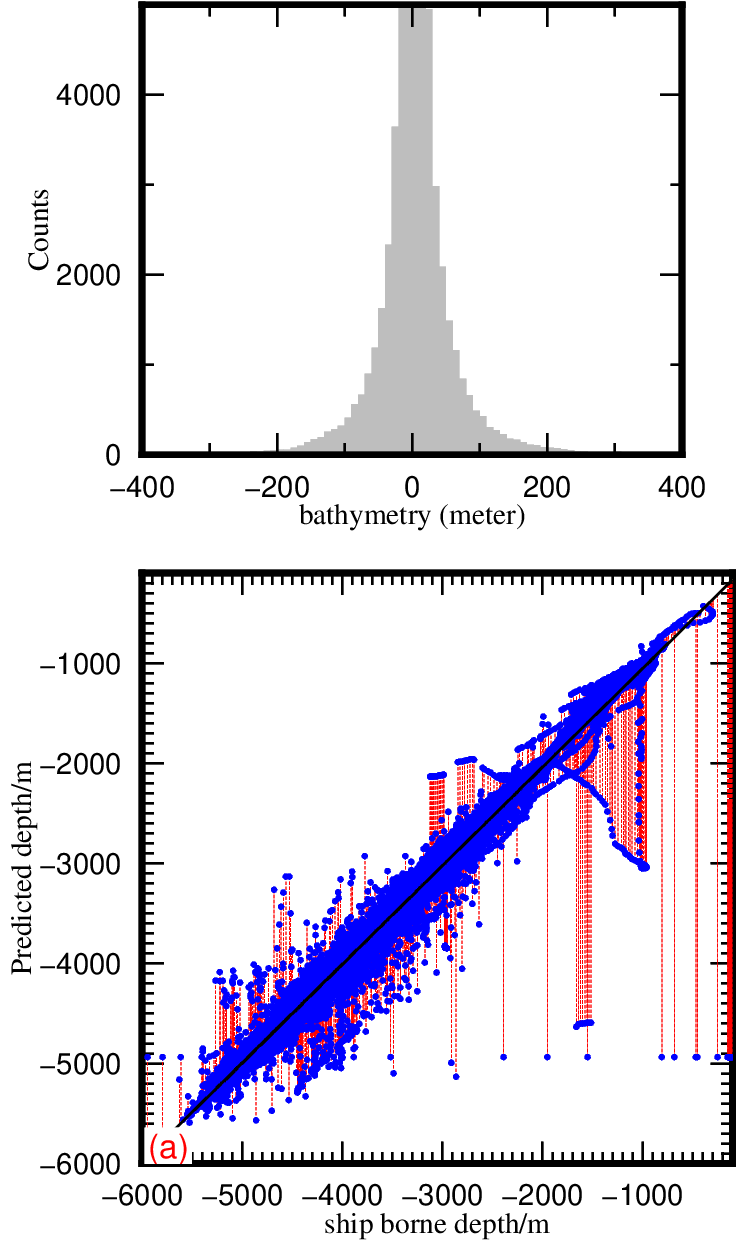
- 短波重力作为输入可以明显提高模型精度,和检核点水深差异的标准偏差为73.5m;不加入短波重力,若使用重力异常、重力梯度和垂线偏差为训练数据,则STD为227m。
- 加入短波重力之后,再加入其他数据作为输入,得到结果几乎一样,即仅使用短波重力一个量就可以得到高精度的水深预测值。
- 使用同样的训练数据和检核数据,GGM和真值差异的STD为85m,即FC-DNN精度超过了GGM。
!注意,为了和已发表论文(
Annan和Wan,2022)的结果比较,上述结果并未进行第一节所展示的数据质控,如果进行数据质控FC-DNN的精度大约在30m,几乎接近当今先进多波束的测量精度!!
CNN
CNN用卷积对图像做操作,将所使用的卷积核看做未知参数,在训练网络的过程中求出最优参数。可能会有人疑问,重力和水深不是图像,怎么用CNN呢?的确,和经典数字识别、猫狗识别完全不同,重力数据是一个网格文件,实测水深是一些船测航迹,本质上没有一连串的同样大小的图像。
使用CNN的思路大概是:每一个水深点有一个经纬度坐标,这个坐标的四周组可成一个4×4大小的二维矩阵坐标,矩阵坐标上可以安置任意的input,比如重力异常、重力梯度、垂线偏差和经纬度,这样形成6个通道(类似图像的RGB通道)的三维张量,然后每一个水深点坐标上都可以组成一个同样大小的二维矩阵,这就形成了一些列的伪图像(四维张量),从而可以满足CNN的训练。
模型架构
这里我们复现Annan和Wan的网络结构:
1 | model = models.Sequential() |
上面有一些CNN架构的知识点,比如池化层,卷积层等等,读者可以轻松从网上查到,这里也不介绍这些内容啦。
训练、预测和评估
读者最好前往开源仓库查看完整代码,并自己运行一下,提高对这些代码的理解。
https://github.com/GenericAltimetryTools/AIBathy/blob/main/Africa_cnn.ipynb
训练
Python代码:
1 | opt = optimizers.Adam(learning_rate=0.001) |
预测
Python代码:
1 | pre_depth = model.predict(x_pre,batch_size=120) |
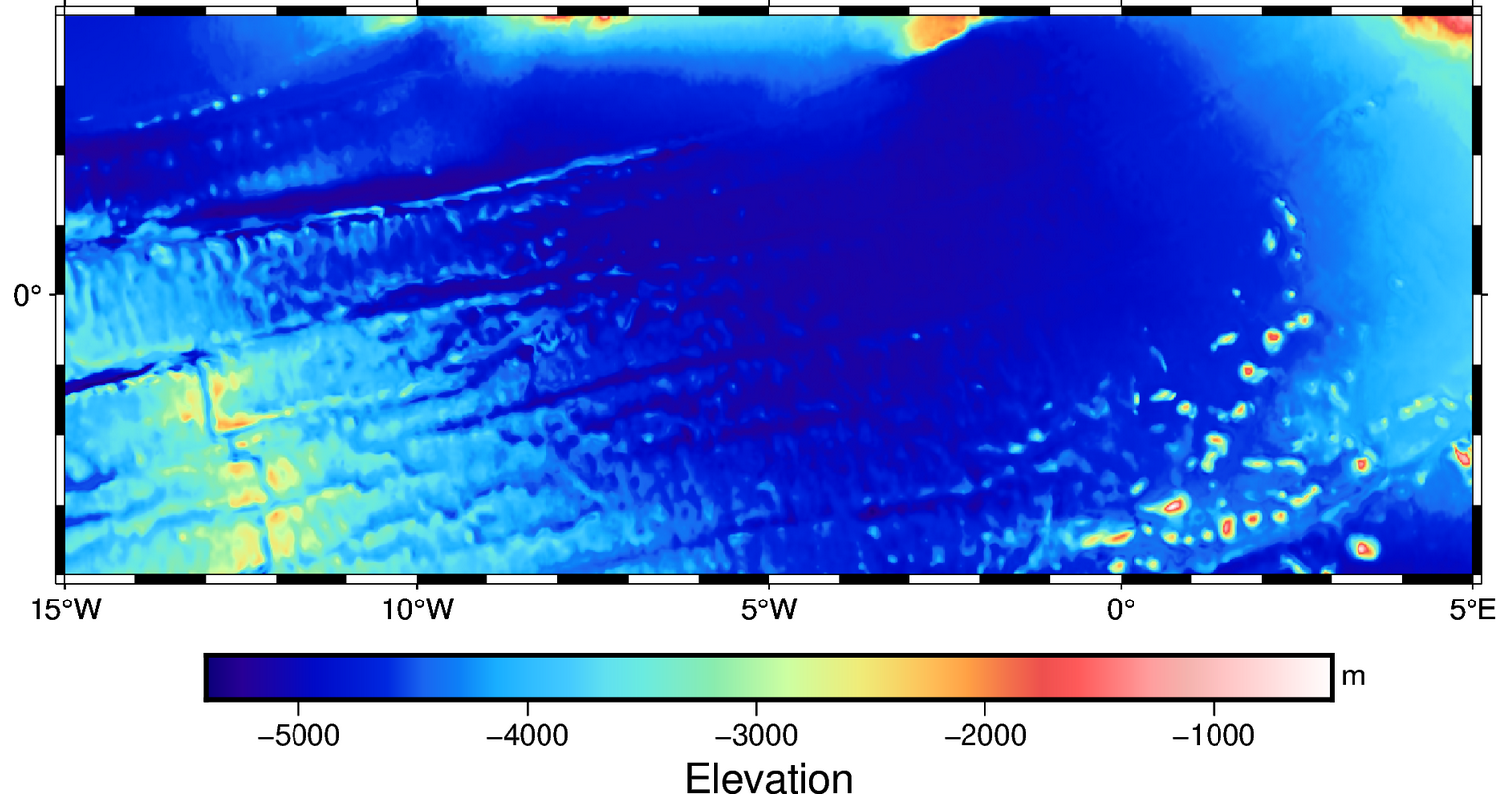
评估
方法和FC-DNN一致。可以使用GMT对输出的水深网格进行评估,或者使用keras内置函数在训练结束后进行评估。 此外我们还可以通过差异直方图、回归分析和功率密度谱等方式对结果进行评估分析,具体代码已上传到Github的fig文件夹。
几点结果
- CNN使用卷积,有固定窗口大小,自带滤波效果,因此预测水深略平滑。使用功率谱分析也表明在短波尺度它不如FC-DNN,但在中间尺度,它的能量高于FC-DNN。
- CNN的精度大概是120 m,这和
Annan和Wan的结论基本一致。 - CNN效果不如GGM,并且差距较大。
- CNN效果不如FC-DNN,这说明高维度的、更复杂的网络并不一定能得到更好的预测结果。
总结
问题答案:
- 物理机制计算的短波重力能提高精度吗?
是 - 高维度的CNN是不是比更低维的DNN好呢?
否 - 人工智能是否比传统方法效果好呢?
是
致谢
深度学习的核心代码由张雨元同学编写,对此小编表示万分感谢。
预告
年底了,人们都更加忙碌起来。距离明年的基金时间也不远了,因此下一系列会关注自然科学基金:
- 国家自然科学基金的海洋遥感、海洋测绘课题资助分析,总体趋势如何?热点领域在哪?
- 卫星测高在哪些领域获得资助,趋势如何?
- 据传,测绘口凡带着深度学习的基金会轻易被毙?是真的吗?原因是什么?