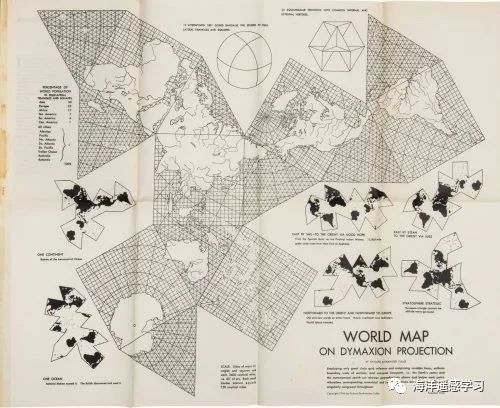
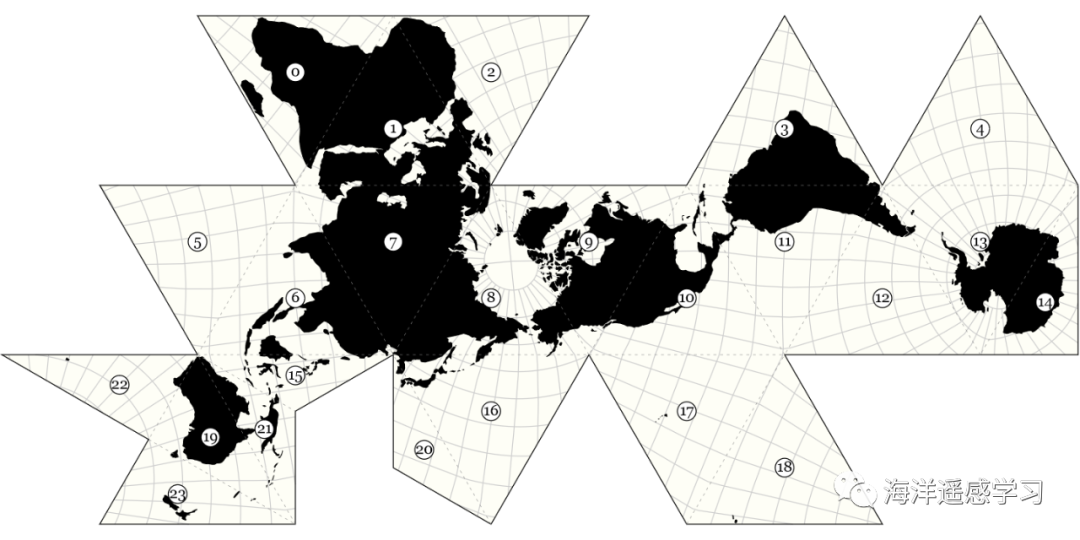
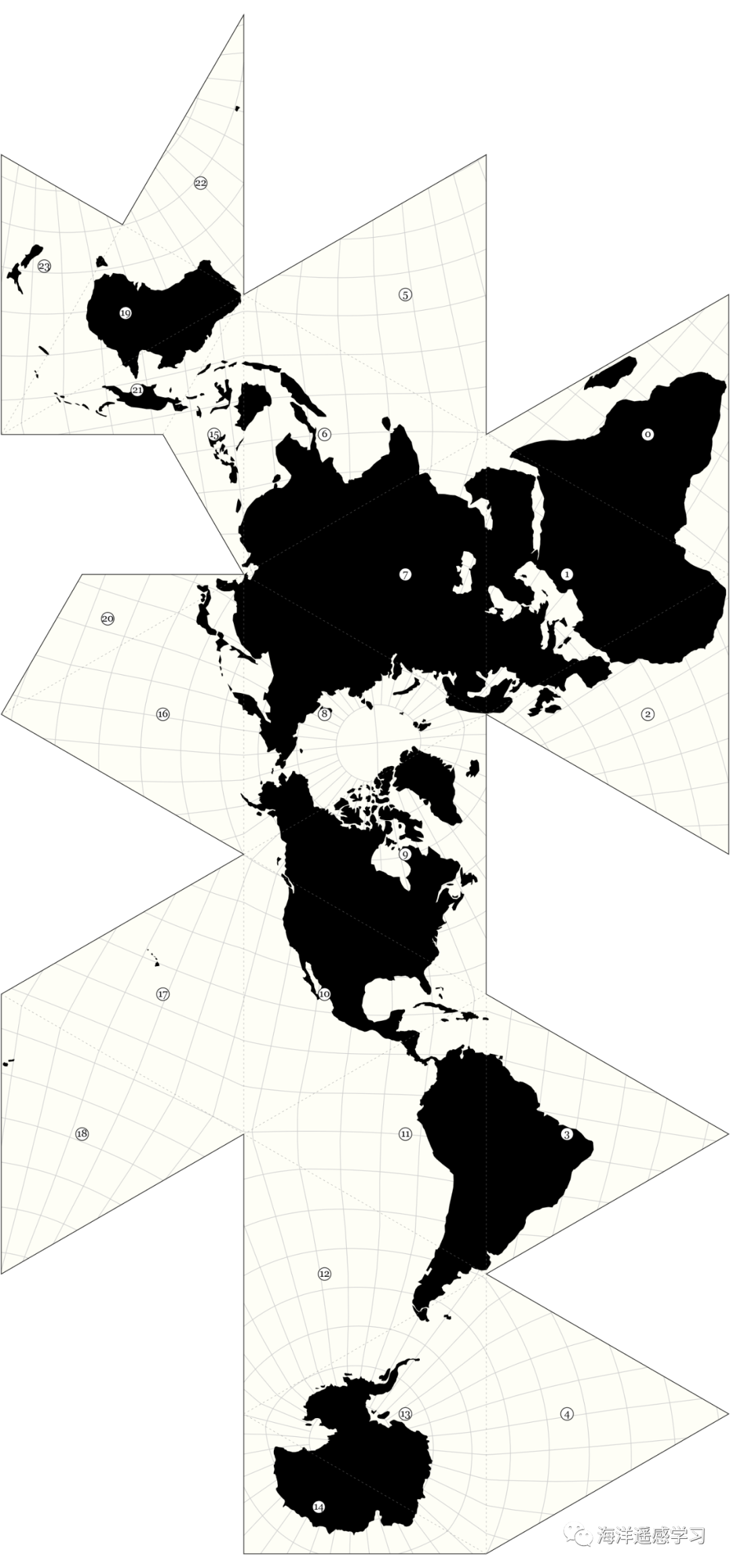
亨利·戴维·梭罗(Henry David Thoreau,1817年7月12日—1862年5月6日),美国作家。1854 年,梭罗出版《瓦尔登湖》,描述他在瓦尔登湖畔度过两年多(1845-1847)的隐居生活。在《瓦尔登湖》中,梭罗以文学家兼自然观察者的身份,细致记录了瓦尔登湖自然现象,他不仅描绘了湖冰从凝结到融化的全过程,还科学地测量了水温、流速和湖底地形,展现了卓越的测绘技能,特别是在水深测绘方面。
尽管梭罗的文学作品直到20世纪初才受到广泛赞誉,但他在生前作为一名测量师就已经颇受认可。梭罗于1862年去世后不久,他的朋友兼导师拉尔夫·瓦尔多·爱默生撰写了一篇纪念文章。爱默生在文章中提到:“梭罗天生就具有测量的才能,这是源于他深厚的数学知识……他在测量领域展现出的精确性和技术技巧赢得了广泛赞誉,他能够轻松找到所有他想要的工作。”
梭罗自己把测量工作视为他与大自然互动的隐喻,他在《瓦尔登湖》中这样描述:多年来,我自视为暴风雪和暴雨的监督者,忠实地执行我的职责;作为测量员,不管是高速公路还是森林小径,甚至所有横跨土地的路径,我都负责测量,确保它们畅通无阻,并在所有季节都架设起桥梁和渡口。这段文字反映了梭罗对自己作为测量师角色的深刻理解,他不仅仅看待这份工作为一种职业,而是作为一种与自然界沟通和理解的方式,没有什么比原始调查更能让人更接近对这片土地和周围环境。
梭罗的身份作为测量员在中国尚未受到广泛关注,这一职业在他的生涯中被相对忽视。然而,正是这一身份深刻影响了梭罗的环境敏感性,并为他的文学创作提供了丰富的灵感和深刻的思考。作为测量员,梭罗亲身体验了自然环境的细微变化和复杂性,这些体验反映在他对自然界的深刻洞察和文学表达中。同时,梭罗也面临着理想与实际工作之间的紧张关系,他需要在谋生的必要性和他对自然保护的深刻理解之间找到平衡。本文旨在通过搜集和整理英文文献与著作,深入探讨梭罗作为测量员的职业生涯对他文学和环保思想的影响。此外,计划发表一系列关于中外历史上著名测绘人物的小传,以加深公众对这一专业领域的认识和理解。
本文主要参考:Thoreau the Land Surveyor, 2011, by Patrick Chura.
梭罗干测绘的时代背景
土地测绘在美国的历史和政治发展中占据着特殊的重要地位,特别是在殖民时代。随着欧洲人对新大陆的定居,美国面临着无限的土地探索机会,而明确的边界划定对于土地所有权至关重要。这使得测绘成为了不可或缺的技术。在美国的永久定居过程中,测量师成为了这一过程的关键组成部分。测量师不仅拥有国家赋予的重要权力,还负责确保测量的准确性和忠于国家的财产定义和分配协议。
美国开国总统乔治·华盛顿的第一份职业便是土地测量,他在15岁时开始学习测量,17岁作为官方测量师。在大约三年的职业测量生涯中,未来的总统完成了至少190次测绘,拥有了超过一千英亩的优质土地。华盛顿证明了早期美国测量师挖掘美洲大陆主要财富源泉的潜力,成为“当时大宗土地投机的初级合伙人”。
梭罗也许是另一个美国最著名的测量员。从他职业生涯开始,梭罗的名字就频繁出现在康科德的财政记录中,通过承担负责任的、专业的、具有法律约束力的行政职能,梭罗与邻近镇的官员就边界位置进行了个人谈判。梭罗的土地测量工作揭示了其与环境保护主义理念和政治立场之间的复杂关系。
梭罗在1846年对瓦尔登湖的调查进行于一个特别的历史时期,这一时期海岸调查在科学期刊和大众文学中频繁受到赞扬。海岸调查最初于1807年由美国国会授权,其主要目的是服务于军事和经济需求。这项工作为制作精确的地图和获取东海岸详细的地理知识提供了基础,对于体系化的沿海防御和保护国家不断增长的商业海运至关重要。梭罗对瓦尔登湖的调查可能受到了这一时期海岸调查的影响,梭罗对瓦尔登湖的详细调查和制图反映了19世纪美国海岸带测绘的时代特征,梭罗的这些工作不仅仅是自然观察的记录,也可能是对当时流行的海岸调查的一种响应。通过详细地测量和绘制瓦尔登湖的地图,梭罗可能在探索自然环境的同时,也在参与那个时代对精确地理信息的追求。
土地测量员

在1856年4月28日,梭罗完成了一份重要的测量图,并亲笔签名。这份手绘的完整测量图至今仍然保存着。图中左上角写着:“位于马萨诸塞州康科德市西南部,属于托马斯·惠勒所有,由H.D.梭罗勘察。”签名中的“H”部分已经被撕掉。该测绘成果显示这块宗地占地26英亩,并详细指出了周边的属性。这份文件的草稿副本现存于康科德公共图书馆。

在康科德地区担任测量师的十多年间,梭罗的事业蓬勃发展,主要归功于他被公认的诚实和准确性。从1849年到他1862年去世之前,梭罗被誉为迅速发展的康科德地区最优秀的土地测量师之一。他之所以能够达到这样的水平,是因为他对工作的热情、诚实以及对测量本身的简单热爱。换句话说,梭罗之所以出色,是因为他没有把测量工作当作一种生意,而是当作一种艺术来对待,他经常被几何的美所吸引,而不仅仅是工作本身。他对一个人职业角色的看法很简单:不要雇佣一个为了钱而工作的人,而要雇佣一个因为热爱而工作的人。
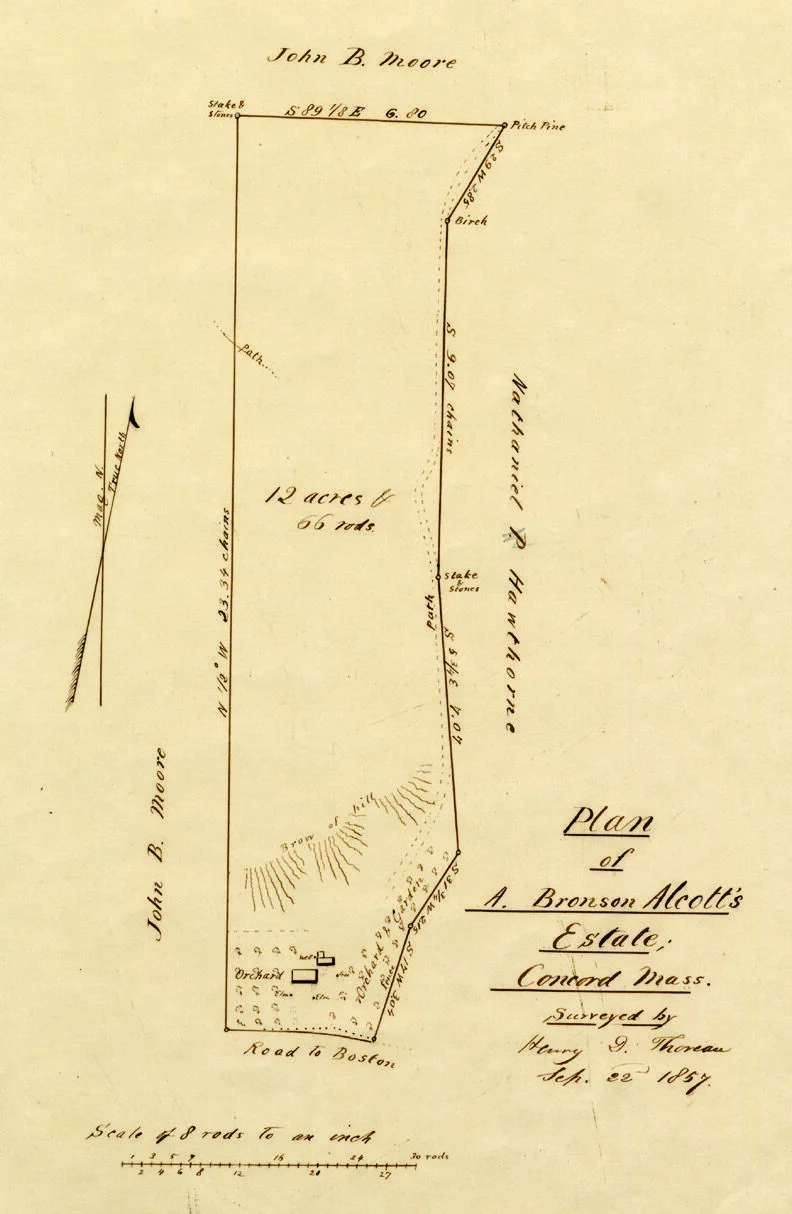
实际上,作为测量员,他的收入超过了从事其他任何职业的收入。他的工作范围包括测量林地、农场、道路和商业地产,因而获得了相对稳定的报酬。有时,当康科德镇的选官向他支付报酬时,这笔钱实际上是直接来自国家。1851年,梭罗作为测量师从康科德镇赚取了六十四美元,主要用于规划道路和测绘边界线。梭罗的测绘活动为他提供了分析环境特征的机会,同时也成为他的主要收入来源。
然而,梭罗的土地测量工作与他的环保主义精神和政治立场之间的矛盾。虽然测量为梭罗提供了分析环境特征和赚钱的机会,但从另一个角度来看,测量工作与梭罗作为自然作家的保护主义核心理念相悖。他在标记和细分瓦尔登湖附近的景观,规划康科德的房屋、谷仓和道路,无疑在一定程度上参与了文明的侵犯和环境的破坏。此外,尽管梭罗在《公民不服从》中表达了对政府权威的强烈反对,但作为测量师的工作实际上使他与地方政府和市政秩序保持了某种程度的联系。通过他的测量工作,梭罗出售他的时间和劳动,参与了土地所有权的确认和财产界线的划分,这些都是建立在财产制度之上的活动,不可避免地与体制发生了一定程度的合作。
瓦尔登湖水文调查

在1845年,年仅28岁的亨利·戴维·梭罗前往瓦尔登湖开始了他的隐居生活。在他的名作《瓦尔登湖》中,梭罗用充满诗意的语言详细描述了他对湖泊自然现象的观察和测量。在调查观测方面,他主要发现了湖冰的波动、风生浪对湖冰的侵蚀作用、冰层水下动力学、湖冰物候差异等。
首先当梭罗在冰面上测量时,他观察到冰面在微风下波动,存在类似于水面的波动。当他的水平仪两脚在岸上,第三脚在冰上,瞄准冰面时,他注意到即使冰面似乎牢固地附着在岸边,但在岸边一杆之远的地方,最大波动量达到了三四分之一英寸,而在中间可能更大。

当我勘察的时候,十六英寸厚的冰层,也像水波一样,会在微风之下有些波动。大家都知道在冰上,水准仪是不能用的。在当我的水准仪的三只脚,两只放在岸上,一只放在冰上,而在第三只脚上瞄准并观察时,冰上的极微小的波动可以在湖对岸的一棵树上,变成数英尺的区别。在湖心的波动,恐怕更大。谁知道呢?如果我们的仪器更精密的话,我们还可以测出地球表面的波动呢。
梭罗还注意到即使在寒冷的气候中,风吹动的水流和水波能够侵蚀周围的冰块。这一发现表明即使在结冰的湖面上,冰层下的水动力学仍然活跃,能够影响冰层的稳定性和厚度。这一点在自然界中是相对不为人所注意的现象,因为通常人们认为一旦湖面结冰,其下的水体就处于静止状态。具体来说,这种现象可能是由于风力作用于水体表面产生水流和波浪,这种水流、波浪可能会沿着冰层下方移动,从而对冰层的下表面产生侵蚀作用。结果,这可能导致冰层的厚度在不同区域出现变化,甚至可能在某些区域形成较薄的冰层,影响冰层的整体稳定性。
另外,梭罗还细致记录了其它发现:
- 瓦尔登湖的独特性:
“这一个湖,从不像邻近的那些湖沼的冰化得那样早,因为它深得多,而且底下并没有流泉经过。”
梭罗指出瓦尔登湖之所以比周围其他湖泊更晚解冻,是因为它更深,且底部没有流动的泉水。这反映了湖泊的深度和底部水源对冰层形成和融化过程的重要影响,深水湖泊由于水体较大,冷却和加热的过程更为缓慢,因此冰层持续时间较长。
- 温度变化对冰层的影响:
“夏季里在湖岸附近,涉水而过的人都知道的,靠湖沼的水要温暖得多。”
梭罗记录了湖泊不同位置的温度变化对冰层厚度的影响,特别是在湖岸附近。在夏季,湖岸附近的水温通常比深水处要高,这意味着春季时,随着气温升高,湖岸附近的冰层可能首先开始融化。
- 湖泊温度的日变化:
“夜是冬季,早晨和傍晚是春秋,中午是夏季。”
梭罗通过对瓦尔登湖一天中温度变化的描述,提出了湖泊生态系统对日温差的敏感性。他将一天中的不同时间段比作一年四季,突显了湖泊温度如何随着日照和气温变化而波动,进而影响冰层的稳定性。
- 冰层跨介质声传导现象:
“湖发射了它的黄昏礼炮,很有定时。”
梭罗描述了冰层在温度变化下产生的声响,如爆裂声和隆隆声,这些声音是气温变化对冰层物理状态产生影响的直观体现。他提到湖泊在特定时间发出的声音,如黄昏时的隆隆声,反映了冰层对气温升降的反应。
瓦尔登湖水下地形
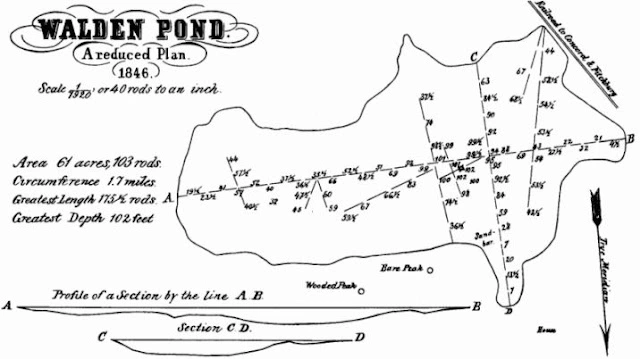
梭罗在《瓦尔登湖》中描写了对湖泊精确的水深测量,这项工作不仅是技术上的挑战,而且成为他个人经验的重要组成部分。梭罗在瓦尔登湖的水深测量工作体现了他的科学思维和方法论。他的测量方法简单却精确,使用钓鱼线和重石作为测量工具,这种方法虽然原始,但在当时是有效的科学实践。通过测量,梭罗确定了湖的最大深度为102英尺,加上水面上涨的五英尺,总深度达到了107英尺。这一发现颠覆了当地人对湖泊深度的传统看法,他们曾误以为瓦尔登湖是无底的。
我用一根钩鳕鱼的钓丝测量了它,这很容易,只需在它的一头系一块重一磅半的石头,它就能很准确地告诉我这石头在什么时候离开了湖底,因为在它下面再有湖水以前,要把它提起来得费很大力气。
在整个过程中,他在瓦尔登湖冬季结冰的湖面上钻了超过一百个深达十六英寸的探测孔。这个艰苦的过程,不仅考验了他的体力,也是对他意志力和专注力的极大挑战。他由此测量了湖的深度,还绘制了湖底地图,并在多个点记录了深度。他发现湖底总体上是规则的,特别是在湖中心,这部分底部平坦且变化不大。他的测量结果表明,湖的最深处恰好位于湖的中心,这一点在湖的最长和最宽处的交点上得到了证实。在测量和绘制湖泊岸线时,梭罗使用了角度交叉的方法,这种方法能够提供令人满意的准确性。梭罗没有沿着湖泊漫长且不规则的周边进行测量,而是利用湖面冰冻的事实,使用从其开阔表面取得的罗盘方位来定位岸线上的选定位置。
在最深的部分,有数英亩地是平坦的,几乎不下于任何阳光下、和风中那些被耕植了的田野。
河道测量

梭罗在1859年和1860年对康科德河进行了深入研究,这项研究几乎成为他的全职工作。他详细记录了河流的环境参数,包括水位变化、桥梁高宽、河床特性、水流情况、洪泛区湿度、水温、浊度以及河谷生态系统的植物。这些记录不仅是他个人和哲学写作的一部分,也成为他参与当地环境政治争议的重要工具。
特别是在康科德河流域的争议中,梭罗被河流草地协会雇佣,为反对大坝建设的案件提供帮助。他测量河流深度和流速,并研究了河流的历史和康科德流域的定居历史。尽管梭罗未直接参与法律争议,但他的工作被视为中立的测量工作,他的签名并未出现在河草地协会提交的任何法律请愿书上。然而,他的工作表明他同情农民,反对破坏草地和河流的公司利益。康科德河流域争议代表了商业工业力量与传统农业的对立,梭罗的兴趣不仅因其法律重要性,而且出于对自然环境的兴趣。梭罗的测量工作反映了他对环境问题的关注以及在理想与实践之间寻求平衡的努力。
当梭罗进行河流测量时,他可能看到了将工程原理付诸实践的机会,这与他的自然科学兴趣相融合。除了支持一个可信的政治原因外,这次测量也是一个挑战,即学习河流的地貌学,同时直接评估工业发展对他的康科德家园环境的影响。但可以肯定地说,他的主要动机远非金钱,因为他在河边花费的时间几乎肯定与他收到的任何报酬都不成比例。
没有原则的生活
梭罗曾面临着理想与实际工作之间的紧张关系,他需要在谋生的必要性和他对自然保护的深刻理解之间找到平衡。尽管梭罗曾经为了金钱进行测量工作,同时也在写作有关自然世界的内容,但他在生命的末期不再觉得有必要将这两个过程分离。相反,他发现自己的测量师和自然主义者身份可以共存,并共同服务于他生活的目的。
梭罗对这一方面的看法在他最后的文章中得到了阐述,这篇文章是死后发表的《没有原则的生活》,它们勇敢地面对作者经济生活中的悖论。1862年2月,随着梭罗的健康迅速恶化,他努力将讲座笔记整合成统一的文章,他作为测量师的工作,以及他长期试图将其与更高法则相协调,成为了他思考的焦点。
《没有原则的生活》是梭罗在充分意识到他即将去世的情况下撰写,强调了人们对测量的看法与梭罗个人测量理念之间的重要差异。梭罗毫不畏缩地将测量描述为“我自己的业务”,并坦率且最终地确认,“我是一名测量师”。