阅读文献综述可快速了解某一领域研究进展,随着各类数据库中文献数量的不断增加,如何全面掌握一个研究领域的进展,最好使用专门的工具。Citespace就是这样的文献分析工具,可支持CNKI、WoS等数据库,具备聚类分析、共现分析、共被引分析、热点趋势探测等功能。目前CNKI已经出现了数千篇专门的Citespace相关论文,但文章结构基本相似,下面是一篇以北极航线为主题的论文综述,一方面可以使读者了解北极航向研究情况,有观点称若北极航线开通,图们江流域的珲春取得与新加坡同等重要地位,一方面也使读者掌握类似文章的架构,以便自己也可以写出此类文章。关于Citespace对CNKI和WoS数据库的处理技巧,后面将慢慢整理分享。
文章来源:王武林,龚姣,王成金.基于CiteSpace的北极航线研究进展与展望[J].资源科学,2020,42(11):2075–2091.
作者:王武林1,2,龚姣2,王成金1,3
1.中国科学院区域可持续发展分析与模拟重点实验室/中国科学院地理科学与资源研究所,北京100101;
2.福州大学环境与资源学院,福建福州350116;
3.中国科学院大学,北京100049
当前北极航线已成为全球航运研究的重要议题,梳理其研究脉络及发展态势,对后续理论研究和实践探索具有重要的借鉴意义。本文以CNKI数据库和WebofScience核心合集数据库中的北极航线相关文献为数据基础,使用CiteSpace绘制国内外北极航线研究的合作网络图谱和关键词共现图谱,阐明北极航线研究的知识结构关系与演进规律。结果显示:国内外北极航线研究分别开始于2007年和1991年,在2014年和2015年成为研究热点,国内研究文献年度分布趋势与国际后两阶段基本一致;各领域学者积极参与研究,国内外发文量最多的学者分别是李振福(大连海事大学)和EhlersS(俄罗斯科学院),研究以个人为主,团队合作较少;大连海事大学交通运输管理学院和RussianAcadSci(俄罗斯科学院)分别是国内外研究机构合作网络的核心,各研究机构间合作较少,跨区域、跨部门合作较少;文献关键词词汇类别日趋多元化,研究主题和研究方法趋于多样化;北极航线研究主题集中在北极航线经济可行性、北极航线对经济贸易和海运网络的影响、北极航线通航环境与安全、国家北极航线政策与实施等方面,国内外研究侧重点有所不同;未来北极航线领域可能出现的研究热点有北极航线与冰上丝绸之路融合、航线人文环境、航线安全、联合研究等。
引言
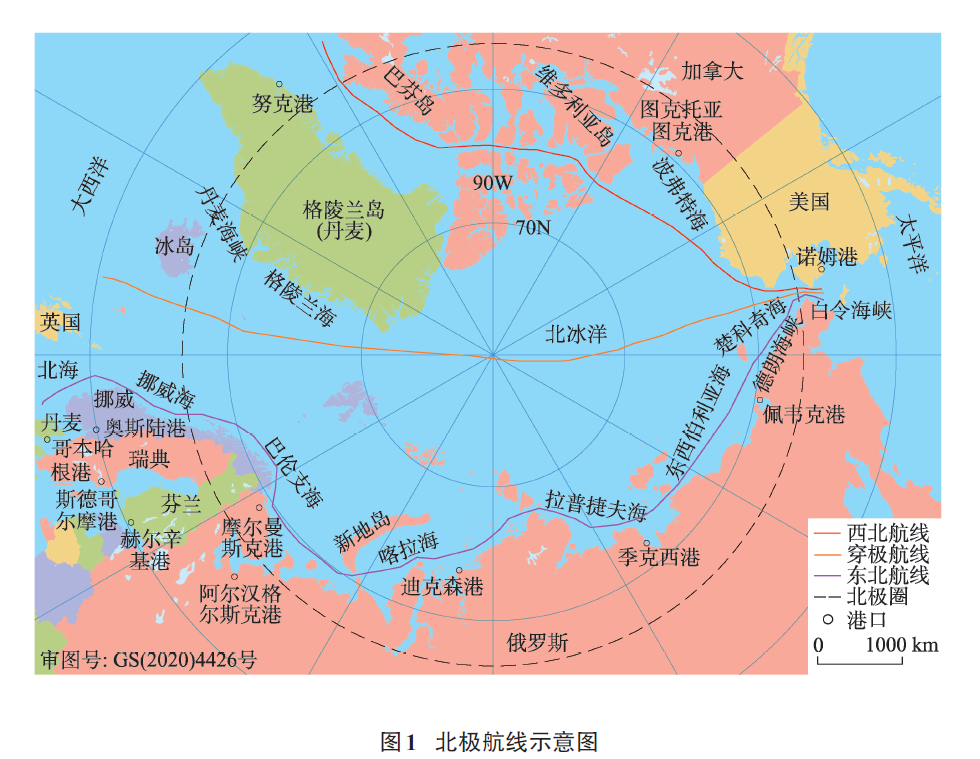
北极航线是指穿过北冰洋并把大西洋和太平洋连接起来的海上航线(图1),包括连接欧亚大陆的东北航线、穿过加拿大北极群岛的西北航线和直接穿越北极点的穿极航线,其中东北航线西起西欧和北欧港口穿过西伯利亚沿岸海域,绕过白令海峡到达中国或日本港口。2007年8月美国宇航局卫星照片显示,东北航线和西北航线首次同时完全融化开通[1],预计到2040年北冰洋将无冰覆盖[2]。2009年夏天,德国“友爱”号和“远见”号两艘货船从韩国经东北航线到达荷兰鹿特丹港,标志着北极航线商业运行阶段的开始[3]。2012年中国“雪龙号”科考船首航东北航线,2017年中国与俄罗斯提出共同打造包括北极航线在内的“冰上丝绸之路”。由此可见,北极航线因经济效益和战略地位而成为国际关注的焦点,近年来,相关研究成果不断涌现,北极航线研究正在成为一个不断发展演进的知识领域,准确把握北极航线的研究进展和学术态势,对后续研究具有重要意义。
北极航线研究领域主题丰富,学科分布广泛,梳理文献可看出,现有研究主要集中在北极航线对国际经济贸易的影响[4,5]、北极航线安全问题[6,7]、北极航线与“冰上丝绸之路”[8]、北极航线的利益和问题[9,10]等方面,这些研究分别从不同视角对北极航线进行分析,但仍缺少对北极航线研究成果的量化分析和综述性评价。本文基于CNKI数据库和WebofScience核心数据库,利用CiteSpace软件的文献计量法,对国内外北极航线研究领域文献进行系统性可视化分析和文献总结,探究北极航线的研究现状,客观揭示该研究领域的态势,为准确评价北极航线研究进展、梳理研究框架、拓展新的思路和方法提供借鉴和参考。
数据来源与研究方法
数据来源
为保证原始数据的准确性和科学性,本文使用中国知网(CNKI)数据库中的期刊文献作为国内中文文献来源,以中文核心期刊、CSSCI来源期刊、科学引文索引来源期刊、工程索引来源期刊为检索对象,检索主题设置为:北极航线或北极航道或东北航线或东北航道或西北航线或西北航道或北方海航道。使用WebofScience核心合集数据库作为国际(含中国)北极航线文献来源,检索主题设置为:“ArcticPassage”OR“ArcticRoute”OR“ArcticSeaRoute”OR“ArcticShippingRoute”OR“NortheastPassage”OR“NortheastRoute”OR“NorthwestPassage”OR“NorthwestRoute”OR“NorthernSeaRoute”。上述两个数据库检索时间都截至2019年12月31日。将检索到的文献进行筛选和整理,去除杂谈、新闻报道、无作者、书评、会议征稿以及明显与主题无关的文献,共得到国内文献282篇和国际文献291篇作为研究样本。
研究方法
本文采用的CiteSpace软件是陈超美教授基于Java语言开发的可视化软件,该软件可绘制某一领域的知识图谱,能呈现和分析该领域学科的结构、规律和分布情况,从而使复杂的信息变得直观和形象[11,12]。但CiteSpace软件仅用于处理文献之间关系,只能计算出该领域重要学者、热点关键词等,具体的文献信息,还需结合文献进行深入阅读。在生成的图谱中,N表示节点数目,E表示连线数量,Density表示网络密度,节点以年轮形式表示,节点半径的大小代表节点出现频次的高低[11]。节点出现突现表示该节点在短时间内出现频率急剧上升,半衰期表示节点在此期间内该保持一定的影响[12]。随后,本文通过系统梳理北极航线相关文献,对北极航线研究主题及相关研究的特点进行总结与解析。
结果与分析
基于CiteSpace的结果统计与分析
发文时间分析
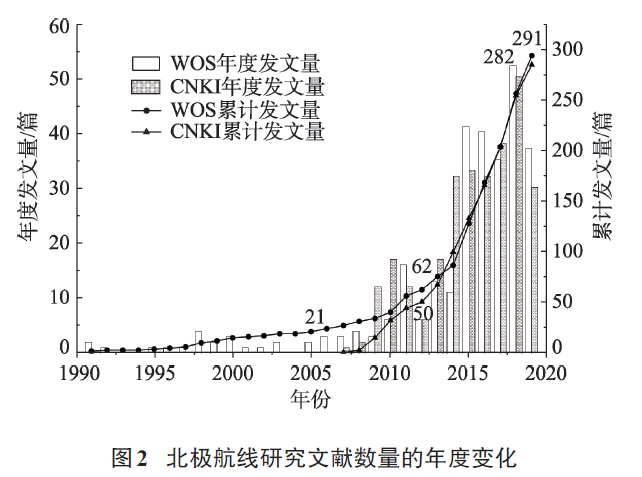
研究文献数量年度分布和变化趋势能够反映该领域的重要性和受关注程度。北极航线研究领域文献数量年度分布如图2所示,总体来看,国内外文献数量均呈现波动增长趋势,2013年后国内文献数量明显增加,2014年后国际文献数量快速增长。从发展阶段来看,国内研究大致可分为平稳发展阶段(2007—2013年)和快速发展阶段(2014—2019年)。平稳发展阶段文献数量波动增加,年均发文量较少,相关研究在国内尚未形成热点,参与研究的学者较少;快速发展阶段年度发文量猛增,并在2018年达到峰值50篇,随着中国成为北极理事会正式观察员国和“冰上丝绸之路”政策的提出,国内对北极航线的研究热度和重视程度不断增加,大量研究成果相继发表。国际研究大致可分为缓慢发展阶段(1991—2009年)、平稳发展阶段(2010—2014年)和快速发展阶段(2015—2019年)。缓慢发展阶段文献数量极少,且以北极航线概况的介绍性文章为主;平稳发展阶段年度发文量呈现出“N”型的分布趋势,发文量比上一阶段稍多且研究主题开始多样化;快速发展阶段年度发文量猛增,并在2018年到达峰值52篇。国际上对北极航线的研究起步较早且较为系统,研究主题与研究成果不断丰富和完善,研究视角和研究方法也日趋多元化。国内相关研究起步较晚,国内的两个研究阶段与国际研究的后两个阶段的发文趋势基本一致,且国内外相关研究均在2018年达到年度发文量的峰值。
发文作者分析
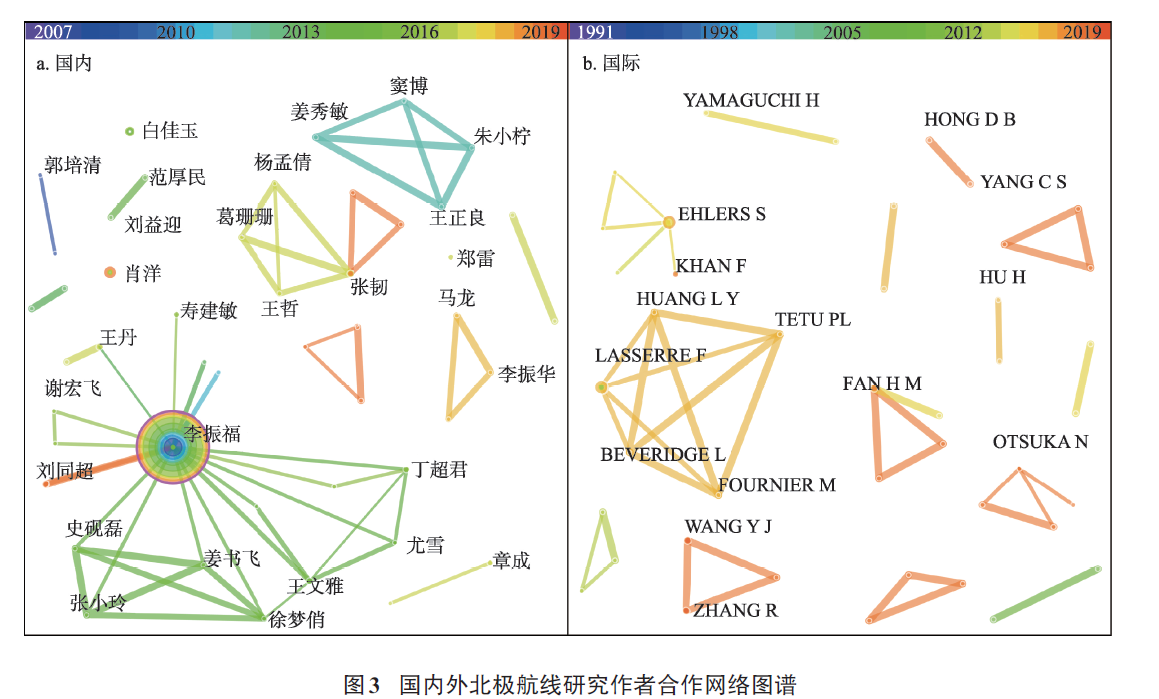
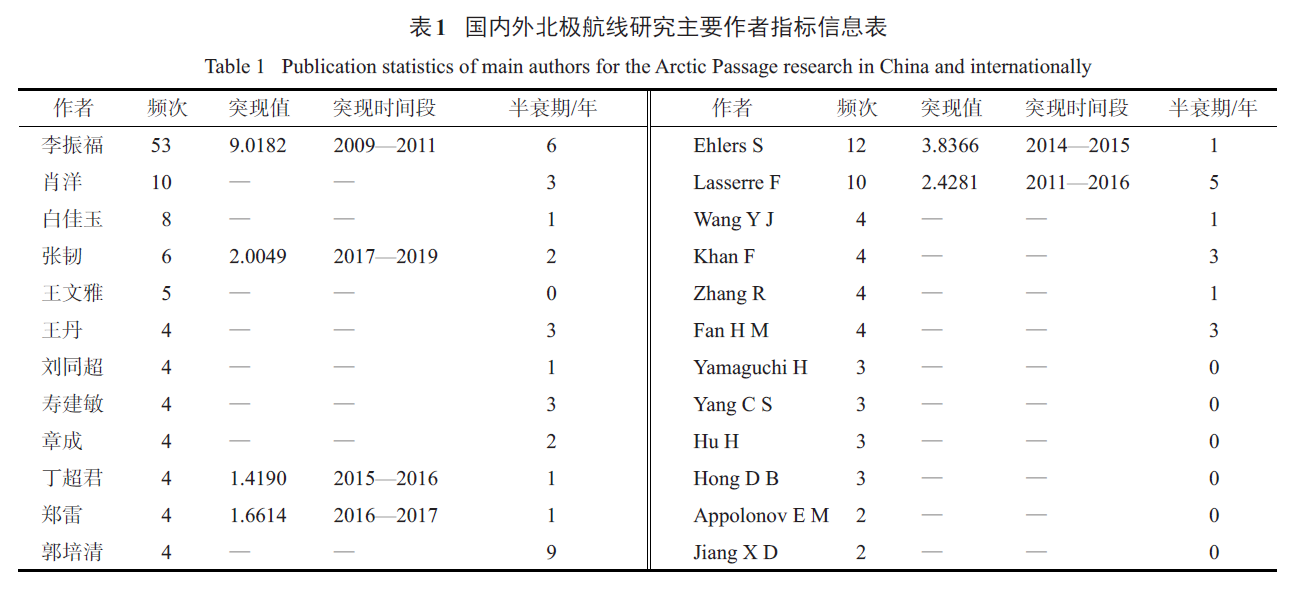
发文作者是科学研究的主体,通过CiteSpace软件的作者合作网络分析可以识别研究领域的核心学者及其合作关系。通过CiteSpace软件计算得到国内外作者合作网络图谱(图3)和主要作者指标信息表(表1),李振福以53篇的发文量居国内北极航线发文学者的第1位,且远超其他学者,是作者合作网络图谱的核心,除李振福外其余发文量在5篇及以上的学者有肖洋、白佳玉、张韧、王文雅。从第一作者发文量来看,李振福、肖洋和白佳玉分别有47、10、8篇,王丹、刘同超、章成、郑雷、郭培清均有4篇。从合作网络来看,国内北极航线研究已形成少数研究团队,但团队之间联系微弱,仍处于相对独立的阶段,学者之间的合作仅限于团队内部,跨团队的合作较少,合作网络表现出大分散、小集聚的特征。从作者的突现性和半衰期来看,影响力较大或期限较长的有:李振福、肖洋、张韧、王丹、寿建敏和郭培清。国内主要学者及其研究主题有:李振福主要研究北极航线地缘政治[13]、北极航线环境[14]、航线开通对中国的影响及中国应该采取的措施[15]等;肖洋主要研究北极航线利益相关国的政策及实施[16,17];白佳玉主要研究北极航线的法律地位及航线治理[18];王丹主要研究北极航线开通对中国及沿线国家的影响[19];刘同超主要研究北极航线安全[20];寿建敏主要研究北极航线的潜力[21];章成主要研究中国北极权益[22];郑雷主要研究北极航线航行自由[23];郭培清主要研究北极航线的法律问题[24]。国际发文量在10篇以上的学者有Ehlers S和Lasserre F,发文量4篇及以上的学者还有Wang YJ、Khan F、Zhang R、Fan HM等。从第一作者发文量来看,发文较多的是Lasserre F、Ehlers S、Wang YJ、Hong DB,分别有4、3、3、2篇。从合作网络来看,学者们呈部分集中、整体分散的状态,已形成以Ehlers S、Lasserre F、Wang YJ、Fan HM为核心的研究团队,团队之间相互独立,未形成合作紧密的网络。从作者的突现性和半衰期来看,影响力较大或期限较长的有:Ehlers S、Lasserre F、Khan F和Fan HM。国际主要学者及其研究主题包括:Ehlers S主要研究北极航线运输模式和风险[25-27]、北极航行船舶[28];Lasserre F主要研究北极航线潜力和经济可行性[29]、航运企业[30,31];Wang YJ主要研究航线规划[32]、北极航线对海运网络的影响[33];Khan F主要研究航运风险[25,34,35];Fan HM主要研究航线通航环境[36]、通航风险[37];Yamaguchi H主要研究北极航线海冰及天气预报[38-40];Yang CS主要研究北极航线海冰识别[41,42];Hu H主要研究航运风险和网络[43]、航线经济可行性[44,45]等。
发文机构分析
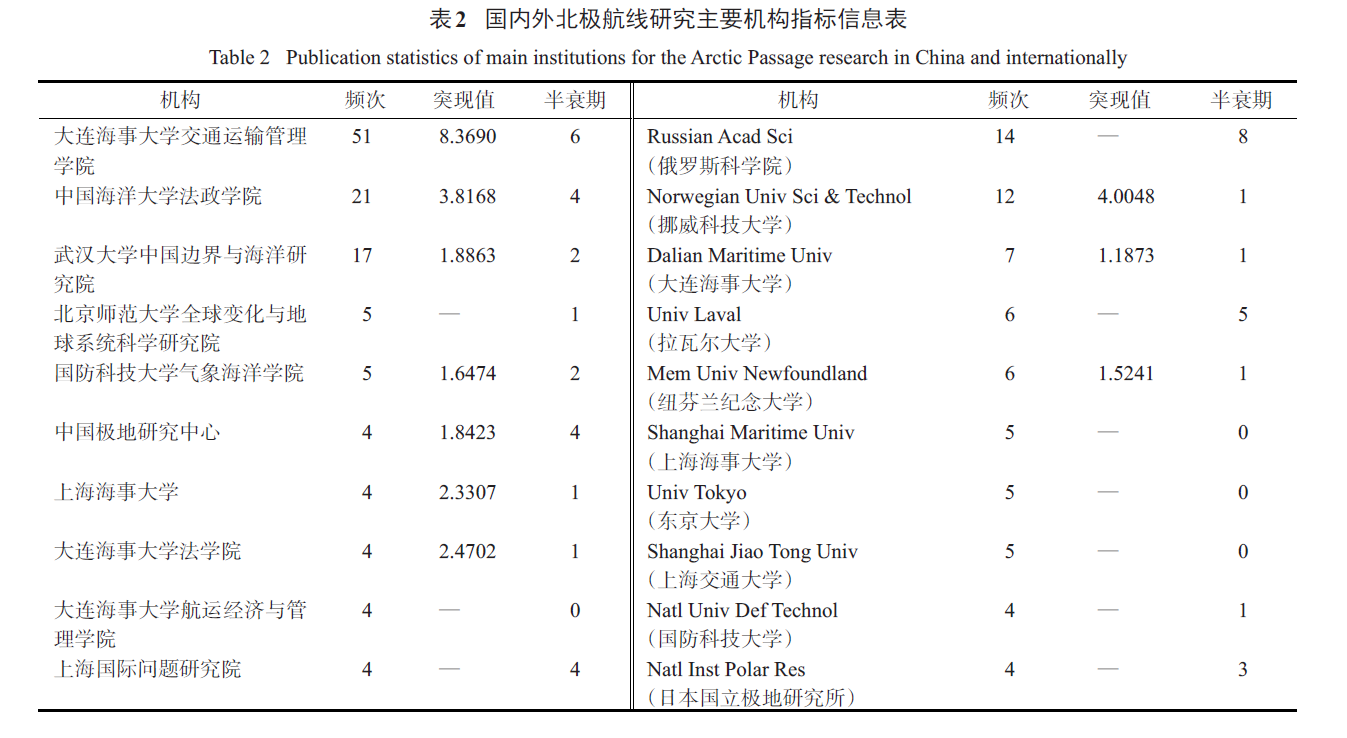
对国内外北极航线文献发文机构进行分析,得到机构合作网络图谱(图4)和主要机构指标信息表(表2)。国内研究机构以大连海事大学交通运输管理学院的发文量为最多,占总文献量的18%。其余发文量在5篇及以上的有中国海洋大学法政学院、武汉大学中国边界与海洋研究院、北京师范大学全球变化与地球系统科学研究院、国防科技大学气象海洋学院。排名前10的机构发文量占总文献量的41%,说明国内北极航线研究机构相对集中,科研成果差异较大。从合作网络来看,研究机构之间的合作少,少量合作均发生在高校内部不同学院和地理位置相近的机构之间,尚未形成较广泛和紧密的学术合作网络。从机构的突现性和半衰期来看,影响力较大或期限较长的有:大连海事大学交通运输管理学院、中国海洋大学法政学院、中国极地研究中心、上海海事大学、大连海事大学法学院和上海国际问题研究院。结合表2可以看出,大连海事大学交通运输管理学院、中国海洋大学法政学院和中国极地研究中心是国内较早介入北极航线研究的主
要机构,武汉大学中国边界与海洋研究院和国防科技大学气象海洋学院是国内近几年才介入北极航线研究的机构。
国际发文量最多的研究机构是Russian Acad Sci,发文量在5篇及以上的机构有Norwegian Univ Sci & Technol、Dalian Maritime Univ、Univ Laval、Mem Univ Newfoundland、Shanghai Maritime Univ、Univ Tokyo、Shanghai Jiao Tong Univ。从合作网络来看,各研究机构之间较为分散,未形成较强的学术合作网络,Russian Acad Sci 是合作网络图谱中大的节点,但未与其他任何研究机构存在合作,其他研究机构之间的合作很少,这些少量的合作大多发生在同一国家。从机构突现性和半衰期来看,影响力较大或期限较长的机构有Norwegian Univ Sci& Technol、Russian Acad Sci、Univ Laval、Natl Inst Polar Res,这些机构是国际北极航线研究的主要力量。从发文量前10的研究机构所属国家来看,中国占4家,其发文量占排名前10机构总发文量的31%,俄罗斯占21%,挪威和加拿大均占18%,日本占13%。发文量排名前5的科研机构所属国家除中国以外,其余均为北极理事会成员国,排名6到10的机构所属国均为北极理事会正式观察员国,这些国家相关科研机构组成了国际北极航线研究的中坚力量。

关键词分析
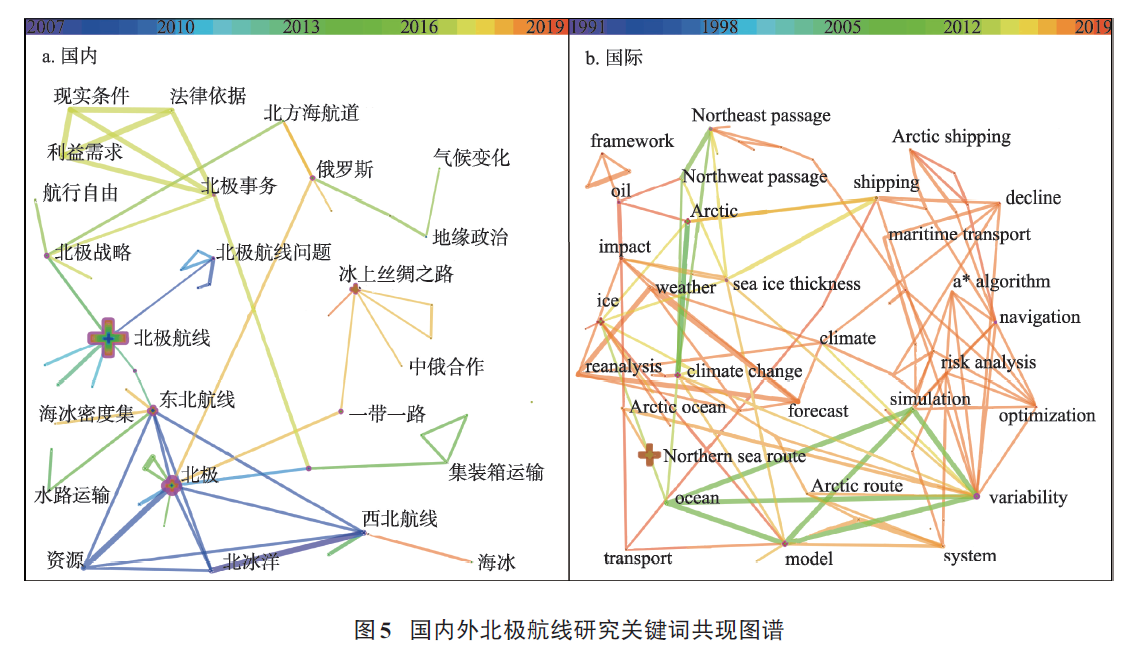
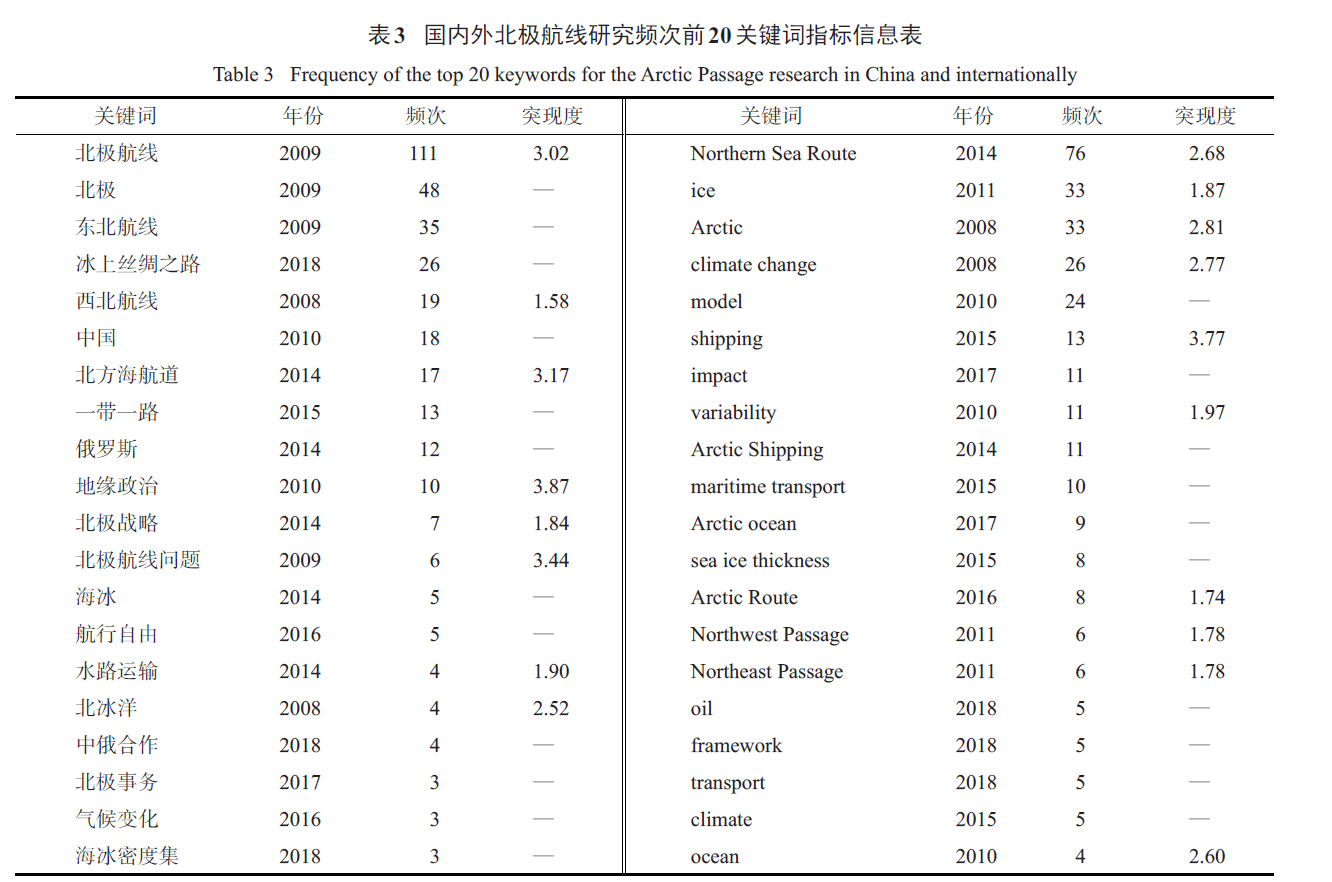
关键词的共现关系是分析该领域研究热点的重要依据,多个节点通过边相连并且聚集在一起,结合频次、突现度等指标信息能够较直观地呈现研究的重要关键词,为明确该领域的研究热点提供依据[46]。通过CiteSpace软件计算并将含义相近的关键词合并,得到国内外关键词共现图谱(图5)和主要关键词指标信息表(表3)。国内北极航线研究关键词共现图谱中最大的节点是北极航线,频次为111,其次为北极和东北航线,频次分别为48和35。近年来随着“冰上丝绸之路”政策的提出,北极航线引发更多关注和研究,关键词词汇类别逐渐多样化,研究主题也呈现多元化趋势。从研究方法来看,前期多采用定性研究方法,近年来多采用定量研究或定性与定量研究相结合的研究方法,随着研究主题的愈加深入,研究方法也愈加多样化。国内北极航线研究领域的重点主题是北极航线对中国的经济发展、沿海港口、航运业等的影响以及中国的应对策略,在高被引Top50文献中有21篇文献涉及了该主题的研究,此外北极航线的经济可行性、北极航线的法律地位、北极航线与“一带一路”的关系、其他国家的北极航线政策也较为重要,在高被引Top50文献中分别有4、4、3、3篇文献对这些主题进行了探讨,可以看出国内研究主要是集聚在北极航线与中国关系的相关研究主题上,其他主题的研究相对较少。
从国际北极航线研究关键词共现图谱连线颜色来看,2013年后的连线数量远多于之前的年份,表明近年出现的关键词数量呈激增态势。北方海航道(Northern Sea Route)是图谱中最大的节点,频次为76,其次为冰(ice)和北极(Arctic),频次均为33。国际研究始于20世纪90年代,前期研究主要集中在北极气候变化、海冰分布、航线通航环境等,近年来关注于北极航线的经济可行性、发展潜力、航行安全与风险、航线开通对北极自然环境和生物的影响等。关键词词汇类别逐渐多样化,研究主题逐渐多元化和分散化。在高被引Top50文献中,北极航线的经济可行性、北极航线开通对环境及生物的影响、北极航线的通航窗口、北极航线海冰分布分别有8、8、5、5篇文献,其余研究主题还包括航运企业对北极航线的态度、航行船舶碰撞、航行风险等。
北极航线研究主题
北极航线经济可行性
相比传统航线,北极航线开通可以缩短西北欧与北太平洋港口之间的海运里程、降低航行成本和时间等,但船舶航行北极航线的运营成本和安全风险远大于传统航线,故其是否具有经济可行性,目前主要存在两种截然不同的观点。首先,北极航线通航具有经济可行性,北纬30°以北任何港口之间使用北极航线要比使用传统航线节省40%的里程,运营成本会相应减少,经济潜力巨大[47],尤其在干散货运输方面,北极航线具有灵活性、敏捷性和适应性等优点[48]。通过对比船舶航行北极航线和传统航线的经济成本发现,在通航期内通过东北航线的集装箱运输航次成本节约10%左右,燃油成本节约35%左右[21];需要破冰服务时北极航线航运利润增加约56%,无需破冰服务时,航运利润增加约105%[49]。北极航线与传统航线联合运输,即在北极航线通航期内使用北极航线、其余时间使用传统航线被认为是一种可行的模式,使用联合运输的北极集装箱服务更加经济[50];Arc7自破冰LNG船全年用联合运输会显著降低运输成本[51];若考虑欧盟征收碳税,联合运输在全年经济测算中必要运费率最低、经济效益最好[52],联合运输可作为未来中国船运企业从中国至欧洲集装箱运输的主导模式[53]。
其次,北极航线开通不具有经济可行性或其经济成本优势需要在一定条件下才能实现。通过北极航线缩短的航运里程并不意味着成本的节省,额外的破冰服务以及适航时间、征费、燃油价格等均会影响航运利润[54],此外还需要对其基础设施和海洋服务提供更多的投资,以确保船舶运输的安全并尽可能减少对环境的影响[55]。尽管使用东北航线能明显缩短航程,但由于全年航次较少,运输成本并无突破性降低[21],加之目前通航船舶体积小、负荷率低,其环境成本高于苏伊士运河航线[56]。北极航线中短期市场小而成本风险大,大多航运公司对其可行性持怀疑态度,在运营初期,大部分东亚和欧洲的航运公司不会使用北极航线[57],只有少数亚洲航运公司对北极航线感兴趣,他们关注于航线的目的地,而非过境航运[58]。如果考虑北极天气和海冰年际变化、俄罗斯收取的费用、石油生产和消费的地理位置、立法问题和基础设施等因素,北方海航道不能替代传统航线[59,60]。北极航线在经济上是否可行与破冰服务成本有关,破冰服务成本越低,北极航线的竞争力越强[54,61],北极航线的经济性还取决于航线的选择[62]。
北极航线对经济贸易与海运网络的影响
北极航线开通将对世界港口航运产生重大影响[63],使之成为连接欧亚海运贸易的关键纽带[55],会对全球经济贸易带来重大影响,能够增加贸易流量并改变贸易流向,从而影响世界贸易格局并促进全球经济增长,东亚、欧盟、北美等将成为最大受益方[64,65]。北极航线带来的经济影响会在地理空间上形成北极航线经济圈,中国、日本、韩国、美国、俄罗斯等国是主要的参与者[66],基于北极航线可划分其经济腹地的范围和等级[67]。作为国际能源运输的新通道,北极航线将在一定程度上改变全球能源贸易的地理方向,使全球能源贸易的来源与通道集中度降低[1],特别是北极石油资源的开发,将对世界石油海运格局产生巨大冲击,预测北极石油海运贸易将占世界石油贸易总量的26.5%左右[68]。此外,北极航线能够加强港口间的联系,增强海运网络的层次性[69],增大中国与加拿大、美国及西北欧海运国家的集装箱海运空间联系强度[70]。未来20~30年间北极航线货流量将快速增长[71],如果实现全年通航,东北航线对全球集装箱货物的配流量将超过一半以上,纬度越高及距离东北航线越近的港口在东北航线的配流量和比例越高[72]。相关研究还模拟了北极航线的经济效益[54,62]、港口枢纽区位[73]、航线竞争力[74]等方面。
中国与欧美的贸易量巨大并不断攀升,这些贸易绝大部分通过海上运输来完成,北极航线的开发利用将会对中国的经济发展带来新动力和机遇。北极航线能提升中国对航线受益国家的进出口潜力[75];提升中国与美国、加拿大和北欧五国的经济联系程度,维持中俄之间原有的经济联系程度[76]。北极航线的开通会扩大中国沿海在连接世界各国海洋航线方面的优势,提高中国北部和东部沿海地区的贸易潜力[5],进而影响沿海地区产业分工和经济发展战略布局[77];也促使图们江流域的珲春取得与新加坡同等重要地位[78]。北极航线还将成为中国石油进口通道之一,将承担中国约7%的石油进口运输量,随着通航环境的改善和极地石油勘探开采技术的提升,该比重会进一步增加[79]。此外北极航线对中国北方港口的竞争程度、网络结构、腹地范围、区位条件等各方面都有一定影响[1,3],尽管东北航线开通不会打破现阶段环渤海港口的整体雁阵模式,但同一层次不同港口的发展位序将会发生改变[80]。
北极航线通航环境与航线安全
(1)航线通航环境
北极航线大部分位于北极圈内,影响其通航环境的因素复杂多变,可将北极航线通航环境影响因素归类为自然环境、助航、人文环境因素3类[14]。在北极航线通航环境影响因素中,海冰是主要的限制因素,关键区域的冰情会直接影响航线的开通,影响东北航线通航的关键区域是东西伯利亚海、新西伯利亚群岛、北地群岛、拉普捷夫海和维利基茨基海峡至谢尔盖·基洛夫群岛[81,82];影响西北航线南线关键区域是维多利亚海峡、皮尔海峡和巴罗海峡;影响西北航线北线的关键区域是麦克卢尔海峡和梅尔维尔子爵海峡[83]。
随着全球气候变暖,北极海冰总量减少而流动性增强,每年通航期内海冰分布范围有所不同,导致航行线路不固定,因此需要加强北极海冰监测和预报能力,为未来航线利用提供保障[83]。近年来各国北极海冰和气象预报水平提升,合作交流扩大,但仍存在观测数据应用不充分、北极中央区预报能力偏弱以及预报信息共享度不够等问题[84]。为了提高北极海冰和天气预报的可靠性,高分辨率的冰海耦合模式[85]、TOPAZ4冰洋资料同化系统[86]以及加入2082北极无线电探空仪观测[39]等模型和方法得到广泛应用。北极航线的通航期随海冰融化而变化,东北航线平均通航期是7月中下旬至10月中下旬[82],全线开通期主要集中在8月下旬至10月上旬,西北航线南线开通期主要集中在8月上中旬至10月上旬,西北航线北线开通时间主要集中在9月[51]。预计到21世纪中叶,北方海航道通航期约23个月,到21世纪末约36个月[87,88]。
北极航线通航带来的诸多污染和干扰,对北极脆弱的生态环境形成严峻挑战,其中最主要的污染来自船舶溢油,具有危害范围广且持续时间长的特点。以FLUENT为研究平台,基于多项因素共同作用下的船舶溢油模型分析溢油在有冰海域中的运动特点[89],或使用高分辨率海洋模型和拉格朗日粒子追踪来模拟污染物的扩散,其扩散的距离高度依赖泄漏发生的地点,在一些地点泄漏的污染物有可能进入深水无法回收[90]。污染和干扰还会对北极生物产生影响,例如在压载舱航行中幸存下来的生物可以建立一个稳定或不断增长的种群,并以压载水为媒介最终成为入侵生物[91]。
(2)航线安全及风险评估
影响北极航线通航安全的因素较多,可将其分为人、机、环境、管理4类,目前环境方面占有较大比例,后期人、机和管理方面占有较大比例[20]。评估北极航行安全和风险的模型和方法包括基于贝叶斯网络的风险模型[34]、统一的态势监测和智力支持系统[92]、基于智能GIS的安全监测方法[93]等。近年来北极水域船舶航行事故数逐年上升,主要发生在巴伦支海东部的俄罗斯摩尔曼斯克港口水域和挪威北部水域[94]。为此学者们提出不同的方法来研究北极海域船舶事故,包括利用模糊事件树分析方法评估北极海域重大船舶事故的风险[95];利用Bowtie关系量化北极水域航行过程中船舶发生事故的概率以及相关的事故后果[25];构建北极地区碰撞与触地故障树来分析海上事故的原因[96]。
破冰船协助船舶通行北极航线是当前主要的通行模式,俄罗斯组建了庞大的破冰船队以维护其北部港口和航线的安全[97],但这种通行模式可能导致破冰船与船舶的碰撞,为了识别破冰船与船舶碰撞危险因素,可建立破冰船与船舶碰撞事故的人为和组织因素专用模型[98],亦可基于船舶跟航理论的不同冰情下安全距离的定量计算模型,量化不同冰情下可接受的安全间隔距离,以及破冰船和护航船舶的运动特性[99],或建立适用于北极航线的交通流跟驰模型,计算船舶安全间距、船头间距、船舶跟驰速度[100]。在关键海峡的自然环境风险评估方面,东北航线的红军海峡、德朗海峡和维利基茨基海峡自然环境风险均逐年下降,通航期内9月自然环境风险最低,7月最高[101];红军海峡自然环境风险减小趋势最大,德朗海峡的自然环境风险度最低,维利基茨基海峡次之,红军海峡风险度最高[102]。此外,北极航线也存在地缘政治安全问题,即北极航线有地缘关系的世界各国在争取北极航线权益过程中涉及和带来的安全问题,其地缘政治格局可以聚类为以美国、俄罗斯和英国为主的国家组成的3个国家集团,为此李振福提出符合北极航线地缘安全需要、有利于维护地缘安全和稳定的“大北极机制”[13,103]。
国家北极航线政策与实施
(1)国际政策与实施
环北极8国尤其是俄罗斯较早研究北极航线,沙俄时代即已利用东北航线运输物资,第一次世界大战之后前苏联对北方海航道进行了科学考察并建立研究机构,为更有效地开发北极航线,俄罗斯实施实际占有战略,试图直接控制北极航线,但由于立法目的不同和国际法与国内法的优先适用问题,俄罗斯的相关国内法规与《联合国海洋法公约》存在严重分歧[104]。在俄罗斯新颁布的法律条文中将破冰船强制领航制度改变为许可证制度,使得外国船只能在北方海航道独立航行,俄罗斯北方海航道政策有进一步向国际开放的政策倾向[105]。余下的北极7国中,冰岛在北极事务中拥有较强的国际话语权,其北极战略是重构外交政策、挖掘北极潜在经济价值和应对北极危机等[106];瑞典强调其与北极历史联系,侧重关注气候与环境、经济发展和人文发展,通过强化与北极国家的合作来提升其在北极的影响力[107];挪威的北极战略是维护国家安全、挖掘经济机遇、提升国际政治影响力[108];加拿大的北极战略目标涉及国家主权、经济和社会的发展、环境保护、地区善治等[109];美国将北极战略嵌入其全球战略之中,以应对气候变化为突破口,获取北极治理的领导权[110]。丹麦国家内部分裂和北极地缘政治的演变,使得其北极战略从温和保守转化为主动进攻[17]。芬兰的北极战略主要侧重于安全和稳定,积极推动北极合作,通过构建北极治理框架实现北极和平发展[111]。
(2)中国政策与实施
作为北极航线延长线上的国家之一,中国正从海运大国迈向海洋强国,开通北极航线对中国而言既是机遇也是挑战[112],《联合国海洋法公约》及其他相关海事条约提供了中国参与北极事务和利用北极航线的相关权利依据,也是实现中国北极权益的科学路径[113,114]。推动航线安全合作是北极国际治理的主要内容,也是中国介入北极事务的最佳切入点之一[115]。目前北极航运治理正处在建章立制阶段,中国可以通过参与构建北极航运国际管制机制,提升中国在北极航运事务治理中的话语权,进而实现和保障中国在北极地区的最大权益[116]。在2017 年发布的《“一带一路”建设海上合作设想》文件中,已经将北极航线明确为“一带一路”的三大主要海上通道之一,同年中俄决定共建“冰上丝绸之路”,该倡议实现了“一带一路”在北极地区的延伸,俄罗斯希望借助中国力量增强在北极地区的活动能力,填补欧洲国家在北极开发合作中的地位和作用[117],而美国对于“冰上丝绸之路”采取竞争性抵制的拒阻思维,可能会导致未来北极地缘政治经济格局出现两种力量并存的趋势[16]。
(3)北极航线法律地位
北极航线法律地位问题是与北极航线相关的最重大国际问题之一,各方主张的法律依据或理论本身缺乏具体标准,相关条约条款在执行实践中存在分歧,并且随着航线通航区域逐步扩大,航线法律地位问题冲突呈现白热化趋势。俄加两国学者从本国利益出发提出了扇形理论、海冰与陆地同权理论、海峡基线法、历史性权利、直线基线法等分别主张东北航线、西北航线是其内水,否认他国船只的无害通过权和过境通行权,而美国和欧盟等则主张北极航线属于用于国际航行的海峡,应开放过境通行,且得到了多数北极圈外国家学者的支持[23,114,118]。加拿大在西北航线管理及主权诉求过程中,通过国内法以环境保护名义间接谋求其西北航线主权地位,并使其国内法相关原则在国际法中得以体现,为本国赢取了航线管理的有利因素[119],俄罗斯以有限开放原则为基础采取选择性妥协治理路径,在航行规则和基础设施建设等问题上主动妥协,将北方海航道作为应对外部挑战和国内发展需求的新增长点[120]。国内有学者认为北极航线应定性为用于国际航行的海峡,北极航线军事演习具有非法属性,军事测量自由是相对性自由,应合理限定冰封区域条款在北极航线的适用[118,121],并确立北极航线特殊条约规制型海峡治理模式[122]。
国内外北极航线研究异同
随着全球气候变暖、北极冰层融化,北极8 国愈加重视北极航线研究,其他利益相关国开始关注北极航线问题,国外关于北极航线议题的研究起步较早,在技术层面和理论层面都有一定程度的积累。国内对北极航线的科学考察和研究相对较晚且理论进展相对迟缓,近年来国内逐渐重视北极航线的研究,对于北极航线的经济性、北极航线治理与中国如何参与治理、北极航线对中国的战略意义以及中国应采取的策略等开展了大量研究,但研究深度和广度以及研究成果影响力与北极8 国相比仍存在较大差距。国内外研究主题基本一致,相较而言在研究方向和研究尺度上存在着较大差异,国内学者大多从国家或地区视角研究北极航线,部分国际学者是以航运公司、托运人等视角进行研究;在航线发展潜力与经济性研究中,国内学者认为北极航线的开通将会给中国以及相关国家带来诸多益处,且会给海运格局带来巨大的变革,国际学者大多认为北极航线目前还不足以对世界经济发展起到推动作用,同时可能会严重破坏北极的生态环境[123];在北极航线通航环境研究中,国内学者主要通过以往的数据来分析通航窗口、关键海域等,国际学者侧重于对未来通航窗口、航线规划、海冰和天气的预测;对于北极航线通航性的研究,国内学者对航线通航性持积极态度,国际学者一般认为航线还处于不安全通航状态之下;在航线安全研究中,国内侧重于航运安全和地缘安全且对航线治理及中国参与航线治理研究较多,国际学者则侧重于提出预测航线风险的方法与模型;在相关国家政策战略研究中,国内学者大多将重点放在俄罗斯且对中俄合作十分注重,其次是对韩国、日本、加拿大等国的研究,国际学者对美国、俄罗斯、加拿大的研究较多。
结论与展望
结论
本文以CNKI 和WOS数据库中北极航线相关文献为研究对象,采取信息可视化研究方法并应用CiteSpace 软件,对国内外北极航线研究的相关文献进行可视化分析和文献评述,研究结果显示:
(1)从年度发文量来看,国内可以划分为平稳发展和快速发展2 个阶段,国际可以划分为缓慢发展、平稳发展和快速发展3 个阶段,国内外北极航线研究的文献数量随着年份变化整体上呈逐渐增长趋势,国内大量文献出现在2013 年后,国际大量文献出现在2014年后。
(2)从发文作者来看,李振福、肖洋、白佳玉、张韧、王丹、刘同超、寿建敏、郭培清是国内北极航线研究的核心作者,Ehlers S 和Lasserre F 是国际北极航线研究的核心作者,国内外均已形成少数联系微弱的研究团队,未形成合作紧密的网络。
(3)从发文机构来看,国内主要发文机构有大连海事大学、极地研究中心、中国海洋大学、武汉大学等,国际主要发文机构有Russian Acad Sci、NorwegianUniv Sci & Technol、Dalian Maritime Univ、Univ Laval、Mem Univ Newfoundland 等,团队内部之间合作关系较为密切,不同团队之间受地域学缘等因素影响,联系强度和合作关系较弱。
(4)从关键词共现来看,北极航线研究随时间变化越来越活跃,关键词词汇类别逐渐多样化,研究主题和方向逐渐多元化,研究方法逐渐深入化,国内外的高被引论文的研究主题不一,国内研究主题相对集中,而国际研究主题较为分散、多元。
(5)从研究主题来看,北极航线研究热点主要聚焦于北极航线的经济可行性、北极航线对世界经济贸易与海运网络的影响、北极航线通航环境与航线安全以及北极航线政策与实施等主题。国内外研究侧重点有所不同,国内侧重于研究北极航线的地缘政治、国家利益、经济贸易、经济可行性,国际侧重于研究航线安全、生态环境、海冰天气预测等,大部分国内学者对航线经济性、通航情况、未来发展持积极态度,而国际学者则较为保守和谨慎。
展望
未来北极航线研究方法和研究视角有待进一步丰富,研究领域和研究深度需拓展和加强。北极航线研究领域未来可能出现的研究热点:
一是北极航线与“冰上丝绸之路”融合问题。已有学者将北极航线与“冰上丝绸之路”进行了联合研究,这是一个新的并可积极拓展的研究方向,在未来几年可能会成为研究热点。
二是北极航线人文环境方面的研究。当前大量研究围绕气候、海冰、水文、物种、生态等自然环境方面进行展开,尚缺少人文环境方面的研究,例如土著人民对北极航线开发的态度以及影响。
三是北极航线安全问题。随着通航窗口的增加,北极航线安全问题愈加明显,未来应重视基于理论视角从微观和宏观方面对北极航线安全问题进行研究。
四是联合研究问题。目前主题联合研究和国内外联合研究还较少。在主题联合研究方面,可将航线经济性和环境影响、航线地缘安全和通航环境安全、国家地区视角和航运公司视角等进行联合研究。在国内外联合研究方面,可与北极8 国进行航线开发、自然生态环境保护、极地船舶技术、北极资源开发等方面研究;可与日本、韩国等航线延长线国家进行合作参与北极事务、利用北极航线等方面研究。





![Temporal and spatial scales for a variety of ocean processes (adapted from Dickey and Bidigare [2005]](/images/sub.webp)