今天分享一位GMT志愿者的动画制作代码,内容和上一篇的地震分布演变类似。
- 代码使用了GMT开发版的功能,建议在Linux下通过源码更新GMT,win下的源码安装稍微麻烦。否则无法得到结果。
- 需要下载地震数据,地址为:https://github.com/GenericMappingTools/gmt/pull/5019
- 这个例子的代码正在快速更新中,问题尚未全部解决,请关注上面的git网址跟踪。
Code
1 | #!/usr/bin/env bash |
今天分享一位GMT志愿者的动画制作代码,内容和上一篇的地震分布演变类似。
1 | #!/usr/bin/env bash |
修淳1,2,王国钢3,杜明1,2,霍素霞1,2,刘莹1,2,陈可可1,2,马芳1,2
作者简介:修淳,博士,高级工程师,主要从事海洋地质学、海域海岛监管技术研究.
摘要:海岸线不仅是海陆分界的重要地理要素,其所属的海岸带也是人类活动最集中的区域。
根据自然资源部关于开展新一轮海岸线修测工作的相关部署,全国海岸线修测工作于2019
年正式启动。本文从地方标准和全国规程的解读入手,结合修测工作实践,分析了修测过程
中的地方标准和全国规程有机结合、复杂区域海岸线类型界定等问题,提出了尽快实施基于
新一轮修测成果的海岸线定期调查更新与自然岸线评估机制、自然岸线占补平衡机制等相关
机制体系研究,旨在为海岸线修测成果报批以及陆海统筹管理提供策略支持。
《海洋学术语 海洋地质学》中将海岸线定义为“多年大潮平均高潮位时海陆分界痕迹
线”[1],尽管其他标准或著述对海岸线的定义描述存在一定的差异,但基本遵循海岸线为平
均大潮高潮痕迹线的本质特性[2,3]。海岸线不仅是海陆分界的重要地理要素,其所在的海岸
带也是人类活动最集中的区域。研究表明,海岸线附近区域的人口密度是世界平均人口密度
的近3 倍[4]。据模型统计显示,2015 年我国海岸带438个统计单元的人口总数约为3.59 亿
人,平均人口密度为6.37 人/公顷[5]。海岸带地区人口的高密度聚集使海岸线资源日益紧张,
也引发了经济、社会和环境等方面的多种问题,如湿地面积骤减、岸线固化比例过多、海水
倒灌加剧等。这也反映出被视为地理指标的海岸线同时还具有与生产生活密切相关的社会属
性。
我国现行有效的海岸线基础数据来源于2007—2008年各省(区、市)人民政府批准公
布的修测成果[6],迄今已过去十多年。这期间随着社会经济发展和海岸带环境变化的影响,
海岸线发生了较大程度的变化[7-9],同时诸如岸线资源粗放式开发、陆海管理交叉等问题的
凸显以及陆海统筹和国土空间规划的需求,都促使亟需开展新一轮修测,以满足新时代生态
文明建设和海洋强国建设要求。2016 年11 月1 日,中央全面深化改革领导小组审议通过了
《海岸线保护与利用管理办法》,这为构建科学合理的海岸线保护与利用格局提供了重要依
据。《海岸线保护与利用管理办法》对开展新一轮全国海岸线调查(修测)进行了明确要求,即“省级海洋行政主管部门会同有关部门开展海岸线调查工作”,“由省级人民政府批准后公
布”。
浙江省和山东省在全国范围内属于较早启动新一轮海岸线修测工作的省份,分别于
2018 年4 月和2019 年6 月年正式实施了本省首个与海岸线修测(调查)相关的地方标准,
即《海岸线调查统计技术规范》(DB33/T 2106-2018)和《海岸线调查技术规程》(DB37/T
3588-2019),这两个节点均早于《全国海岸线修测技术规程》的印发时间(2019 年7 月)。
山东省已于2019 年10 月前完成了新一轮海岸线修测外业测量和内业制作工作。本文从地方
标准和全国规程的解读入手,结合现场修测实践,提出了本次海岸线修测工作中的几点思考
和建议,旨在为海岸线修测成果报批、陆海统筹管理、国土空间规划等提供策略支持。需说
明的是,本文提及的海岸线主要指大陆海岸线,海岛岸线不在本次讨论范围内。
如前所述,浙江省和山东省地方标准的发布和实施时间以及全面开始海岸线现场测量的
时间均在全国规程印发时间之前,因此其海岸线修测依据实际上是以地方标准为主、全国规
程为辅。尽管地方标准与全国规程在海岸线分类、位置界定、自然岸线保有率统计等方面存
在一定程度的差异(另有详文述及),但为了贯彻落实自然资源部关于开展海岸线修测工作
的相关部署,在后期成果制作过程中仍按照全国规程对修测数据进行了局部调整。
需注意的是,沿海个别省份在近几年就已经启动并完成了海岸线修测工作,也有省份正
式发布实施了与海岸线修测(调查)相关的地方标准。这些已正式生效的地方标准相对全国
规程应能更好地体现当地的实际情况。如果“一刀切”式地要求已完成岸线修测工作(前提
是依据生效的地方标准)的省份按照全国规程进行全面的修改,会造成大量的重复性工作以
及人力、物力的较大浪费。因此,如何根据本省海岸线的实际情况,做到地方标准和全国规
程的有机结合是早先已完成海岸线修测工作的省份需要深入思考的问题。事实上,目前已实
施的地方标准和全国规程在本质上并无冲突,两者在一定程度上可相互辅成,共同致力于界
定出一条符合本省实际情况和海陆统筹管理要求的海岸线。
通过海岸线修测实地踏勘发现有一种海岸线界定情况值得进一步商榷,即可自然纳潮的
土质围堤养殖池岸线类型界定。根据全国规程,可自然纳潮的土质围堤养殖池的岸线位置应
界定在养殖池向陆一侧的堤坝前沿处,岸线类型为人工岸线(一级类)、围海(二级类),但
实际上养殖池的向海侧和向陆侧围堤均为土质堤坝,并不符合规程中对于人工岸线的定义—
—由永久性构筑物组成的岸线。这类养殖池塘靠陆一侧的岸线一般多为自然或半自然状态下的泥质岸线,具有破损程度较高、生态功能较差等特点,如果后期实施养殖设施拆除,可一
定程度上恢复自然岸线原貌及属性,破损严重岸段可进行整治修复。针对这一问题,建议围
海养殖向陆一侧的岸线类型界定应以事实为准,不能简单地全部界定为人工岸线。例如,如
果该区域有已批准的整治修复方案或开发利用规划,则根据具体方案规划可将岸线类型界定
为自然岸线或生态恢复岸线,纳入自然岸线管控及保有率统计之中;如果没有任何方案规划,
则以便于统一管理、避免岸线细碎化为原则,可参照相邻岸线类型界定为自然岸线或人工岸
线。
本次海岸线修测距离上一次修测已过去十余年,沿海各省(区、市)的海岸线长度和形
态发生了较大程度的变化,如果将海岸线修测更新周期设置为每十年一次明显不符合新时代
生态文明建设和海洋强国建设要求。环保督察和海洋督察期间发现部分地区存在海岸线向海
一侧管理交叉等问题,也不适应海陆统筹管理战略部署。在《国务院关于加强滨海湿地保护
严格管控围填海的通知》(国发〔2018〕24 号)要求下,以往粗放式的围填海开发利用活动
得到了有效管控,但由于自然因素干扰或重大战略项目实施导致的岸线变化的可能性仍在存
在。因此在本轮海岸线修测成果支撑下,结合各省(区、市)实际情况,有必要建立海岸线
定期调查更新机制,明确更新周期,完善海岸线调查体系和评估机制。更新数据得到具有资
质的测绘质量检验部门检定合格后,由自然资源主管部门及时发布,实现海岸线的精细化管
理。同时,基于定期更新的数据,建立自然岸线现势数据库,全面分析自然岸线稳定性,客
观评价自然岸线质量,科学选划潜在的生态修复岸线,为各级海岸线保护与利用以及自然岸
线保有率管控提供翔实数据。
以山东省为例,本次修测发现沿海各市在海岸线开发程度和质量等方面差距较大,导致
现存的自然岸线保有量在东西地区之间以及黄渤海之间差距明显,自然岸线保护仍面临多方
面压力。例如,某一地区自然岸线保有率较低,但并不意味着岸线开发质量高;某一区域海
岸线开发利用程度和质量均较好,自然岸线保有率却不低。自然岸线保有率目标是海岸线保
护的底线,是海岸线开发利用不可逾越的红线,为加快推进区域协调发展战略,建议尽快研
究建立适用于本省实际情况的自然岸线占补平衡机制,加快制定占补平衡标准。占多少、补
多少,甚至加倍补;补的不仅是数量,更应注重质量;实行资金补偿、修复补偿、异地补偿
等多种模式,共同确保自然岸线保有率不降低,海岸线总体质量不降低。
需进一步说明的是,广东省自然资源厅于2019 年4 月就《广东省海岸线使用占补制度实施意见(试行)》面向社会公开征求意见,明确了岸线整治修复的原则、措施,规定了岸
线占补流程、岸线整治修复工程竣工验收等,其中就包括 “按照占用自然岸线1:1.5 的比例、
占用人工岸线1:0.8 的比例整治修复岸线”。这标志着广东省在推行海岸线占补机制方面走在
了前列,同时也为其他省份制定海岸线占补平衡机制提供了重要参考。
目前,沿海各省(区、市)海岸线修测成果已处于提交审查阶段,计划在2020 年底公
布。在《海岸线保护与利用管理办法》、《国务院关于加强滨海湿地保护 严格管控围填海的
通知》等相关政策文件要求下,不仅应修测出一条符合技术规范要求、利于陆海统筹管理的
海岸线,更将严格保护海岸线这一理念根植到各级主管部门的管理理念中,切实提高海岸线
管理水平。建议加快新一轮海岸线修测成果转化与应用,推动海岸线保护规划编制工作,坚
持陆海统筹,按照“一线(即海岸线)管控、两域(即海域与陆域)对接”的总体思路,划
定严格保护、限制开发、优化利用岸线类别,构建科学合理的自然岸线保护格局;坚持区域
化、一体化整治修复思路,开展海岸线形态和生态功能修复,提高海岸线总体生境质量,不
断推进我国海岸线综合治理体系和治理能力建设。
海岸线作为海陆分界线,兼具地理和行政双重属性。随着人为活动和自然因素的影响,
近十余年海岸线发生了较大程度的变化,开展新一轮海岸线修测势在必行。
新一轮海岸线修测严格按照技术规程开展,外业和内业工作已全面完成,修测成果正处
于提交审查阶段。在工作开展过程中,地方标准与全国规程的有机结合、复杂区域的海岸线
类型划分等问题对修测成果具有重要影响,需综合考虑分析;同时,随着下一步修测成果的
公布,与之相关的海岸线定期调查更新与自然岸线评估机制、自然岸线占补平衡机制等相关
机制体系研究应尽快提上日程。
修淳,王国钢,杜明,霍素霞,刘莹,陈可可,马芳.新一轮海岸线修测工作中的几点思考[J/OL].海洋开发与管理:1-5[2021-03-24].http://kns.cnki.net/kcms/detail/11.3525.P.20210120.1025.006.html.
《海洋遥感数据共享》高度重视版权,对于来自期刊媒介的稿件,会在文章开头显著标明出处,以表达对作者和平台版权的充分尊重和感谢。
文质彬1,吴园涛1,李琛1,殷建平2
作者简介:文质彬(1984年—),女,四川省成都市人,硕士,研究方向:主要从事光电空天领域重大任务管理工作。email: zbwen@cashq.ac.cn。
通信作者:殷建平 email:yjp@scsio.ac.cn
海洋科学是一门依赖于观测的学科,卫星是海洋研究的重要观测平台之一,海洋卫星数据在海洋科学研究中具有重要的意义。本世纪初以来,我国陆续发射了多颗专门用于海洋观测的卫星,初步拥有了了自主海洋卫星全球观测网络。本文针对国内外海洋卫星资源基本情况,研究分析了我国海洋卫星数据应用发展现状,特别是在海洋卫星数据接收、处理、管理、应用等方面的情况,提出了我国海洋科学研究对卫星数据的科研需求,探讨了我国海洋卫星数据科学应用存在的问题和发展策略。
为服务海洋经济与海洋科技的发展,国内外众多机构不断增加发射海洋卫星,卫星数据资源不断丰富,数据精度及应用的深度和广度也不断增强并日臻完善。利用海洋卫星可开展海洋水色、海洋动力、海冰、台风、海洋渔业等业务化应用,在海洋环境保护、海洋预报(刘娜等,2018)、海洋监测与减灾防灾(蒋兴伟等,2019;林明森等,2018)、海洋资源开发(官文江等,2017)、海上公共安全与重大工程建设、海洋科学研究和区域海洋应用等各方面都发挥了重要的作用。伴随大数据时代的来临,海洋卫星数据的应用前景广阔。本文总结了国内外海洋卫星的基本情况和我国海洋卫星数据应用发展的现状,在此基础上提出我国海洋卫星数据应用发展中存在的主要问题,并提出未来的发展策略。
全球航天大国均具有较为完备的海洋空间观测系统。作为世界航天最强国,美国从20世纪70年代就发射了专门的海洋卫星,首颗专门用于海洋观测的卫星SEASAT于1978年成功发射,40年来发展了海洋环境、海洋水色、海洋动力等不同类型的专用海洋卫星,实现了从空间快速获取海洋信息的强大能力,并形成了多种业务应用。我国海洋卫星发展起步较晚,本世纪初才发射第一颗海洋卫星HY-1A(蒋兴伟等,2008)。我国海洋卫星发展迅速,已经逐步构建起我国自主海洋卫星的全球观测网。目前海洋卫星系列已经成为我国卫星对地观测系统的主要组成部分,也是《国家民用空间基础设施中长期发展规划(2015-2025)》中遥感卫星的重要组成部分。“十三五”到“十四五”期间,我国将要发射10颗以上海洋系列卫星或以海洋为主要应用方向的卫星;到2025年,我国将建立完备的海洋卫星体系。
国际上的海洋卫星大体分为三类:海洋水色卫星(如SeaWiFS)、海洋动力环境卫星(欧洲中心的Jason系列卫星)、海洋综合探测卫星(如Sentinel-3卫星)。海洋水色卫星是对海洋水色要素(如叶绿素、悬浮沙和可溶性的有色有机物质等)和水温及其动态变化的探测(Hooker等,1993; Gregg 等1998)。有效载荷通常选用灵敏度高、信噪比高、光谱分辨率高、波段多、带宽窄的海洋水色扫描仪(张可立等,2018)。通常空间分辨率在300-1000米,地面覆盖周期2-3天。发展海洋水色卫星的目的在于掌握海洋初级生产力分布、海洋渔业及养殖业资源状况和环境质量,了解河口港湾的悬浮泥沙分布规律,监测近海溢油(孙乐成等,2019)、赤潮富营养化、循环水排海热污染、海冰冰情(张树德等,2019)、浅海地形等。海洋动力环境卫星是对海洋风场、海面高度、浪场、流场以及温度场等动力环境要素探测的卫星(林明森等,2018),有效载荷通常是微波散射计、微波辐射计、雷达高度计等,并具有多种模式和多种分辨率。发展海洋动力环境系列卫星的主要目的在于利用微波散射计监控全球海洋表面风场,得到全球海洋上的风矢量场和表面风应力数据,利用雷达高度计提供全球海洋地形数据,得到全球高分辨率的大洋环流、海洋大地水准面、重力场和极地冰盖的变异等(Chelton, 1985)。海洋动力环境卫星获取的实时高精度海面动力和海底拓扑资料,具有重要的战略价值。海洋综合探测卫星是对全球与近海(包括海岸带)海洋动力环境和生态环境各种信息的综合遥感监测,同时具备多种载荷。有效载荷包括可见光、红外,主动、被动遥感器,如多光谱成像仪、合成孔径雷达、微波散射计、辐射计、高度计等(Donlon等,2012)。发展海洋环境综合卫星的主要目的在于提供全天时、全天候海况实时资料,用于改进海况数值预报模式,提高中长期海况预报准确率。同时提供海上目标、海岸带调查、海洋污染的实时同步海洋要素,为海洋环境监测、维护海洋权益和海岸带资源调查、综合利用与管理服务。
目前国外主要海洋卫星包括美国SeaWiFS、MODIS、VIIRS,欧洲空间局的MERIS(陈双等,2014)、Sentinel-3卫星,韩国静止轨道卫星GOCI(李冠男等,2014),用于海洋水色的测量。例如:用于测量全球海表温度AVHRR系列卫星;用于构建海面高度数据的TOPEX/POSEIDON(陈双等,2014),Jason-1/2/3和ERS/Envisat 等多颗高度计卫星;用于提取海面高度的GRACE和CHAMP重力卫星,用于海面风速测量的快速散射计QUICKSCAT卫星,用于海面风速、降雨和海温反演的卫星AMSR-E、AMSR-2、WindSat、TRMM等,用于海面盐度(电导率)反演的美国Aquarius和欧空局的SMOS卫星,用于海冰参数测量ICESat,CryoSat-2,SSM/I、SSMIS等(蒋兴伟等,2018)。
同时,很多陆地卫星也用于海洋的研究中,包括传统的陆地卫星Landsat系列(段广拓等,2018),高分辨率光学卫星SPOT、Quickbird,Pleiades以及Worldview系列卫星,用于海面目标、近海岸带生态系统、海岛以及海岸线变迁研究;一些高分辨率雷达卫星,如加拿大Radarsat系列卫星,德国TerraSAR-X / TanDEM-X卫星,ENVISAT-ASAR,Sentinel-1等卫星,可用于海面粗糙度、海浪谱估算等的海洋动力过程研究。
国外海洋卫星发展形成了多种海洋业务化的卫星数据产品。包括:以海面风场、海浪、海表层流、海面温度、水汽含量等为代表的海洋动力环境及多源遥感融合数据产品;以叶绿素、有色溶解有机质、悬浮物、初级生产力、光合有效辐射等为代表的海洋光学参数、海洋生态环境参数及其衍生的(如海洋渔业)等遥感产品;以海底地形、重力场等为代表的海洋地球物理产品。
我国海洋卫星包括海洋水色卫星星座、海洋动力卫星星座和海洋监视监测卫星3个系列。海洋水色卫星是以可见光和红外成像观测为手段的海洋遥感卫星。我国海洋水色卫星星座的发展包括3个阶段。第一阶段:海洋1A和海洋1B卫星。其中,海洋1A卫星作为试验型业务卫星,有效载荷包括1台十谱段海洋水色水温扫描仪(COCTS)和1台四谱段海岸带成像仪(CZI),对中国邻近海域的重访周期为3天。海洋1A卫星在轨运行685天,成像约1900轨,在海洋环境保护和海洋科学研究等领域发挥了重要作用。海洋1B卫星是海洋水色系列卫星的第二颗实验星,同样装载了1台十谱段海洋水色水温扫描仪(COCTS)和1台四谱段海岸带成像仪(CZI),可实现对中国邻近海域的每天重复观测。海洋1B卫星在轨运行8年10个月,共成像19233轨,获得原始数据8.84TB。第二阶段:海洋1C和海洋1D卫星。其中,海洋1C卫星于2018年9月成功发射,是中国海洋系列卫星的首颗业务卫星。海洋1C卫星上的COCOTS信噪比大幅提升,可以分辨出更加细微的水色变化;CZI的空间分辨率提高到50米,卫星技术状态达到了国际先进水平,能够提供每天全球海洋空间全覆盖海洋水色卫星资料;海洋1D卫星于2020年6月成功发射,将与海洋1C卫星组网运行,开展大幅度、高精度、高时效观测,具备全球1天2次的水色水温探测覆盖能力,使海洋观测更加全天候。第三阶段:为实现国产水色卫星技术性能和应用能力达到国际先进水平的新一代水色卫星,包括正在规划的静止轨道卫星及预计于2022年发射的新一代HY1E卫星,后者将实现全球海洋水色的高空间分辨率,高光谱分辨率观测,相应载荷已经在“天宫二号”进行了实验(林明森等,2019)。
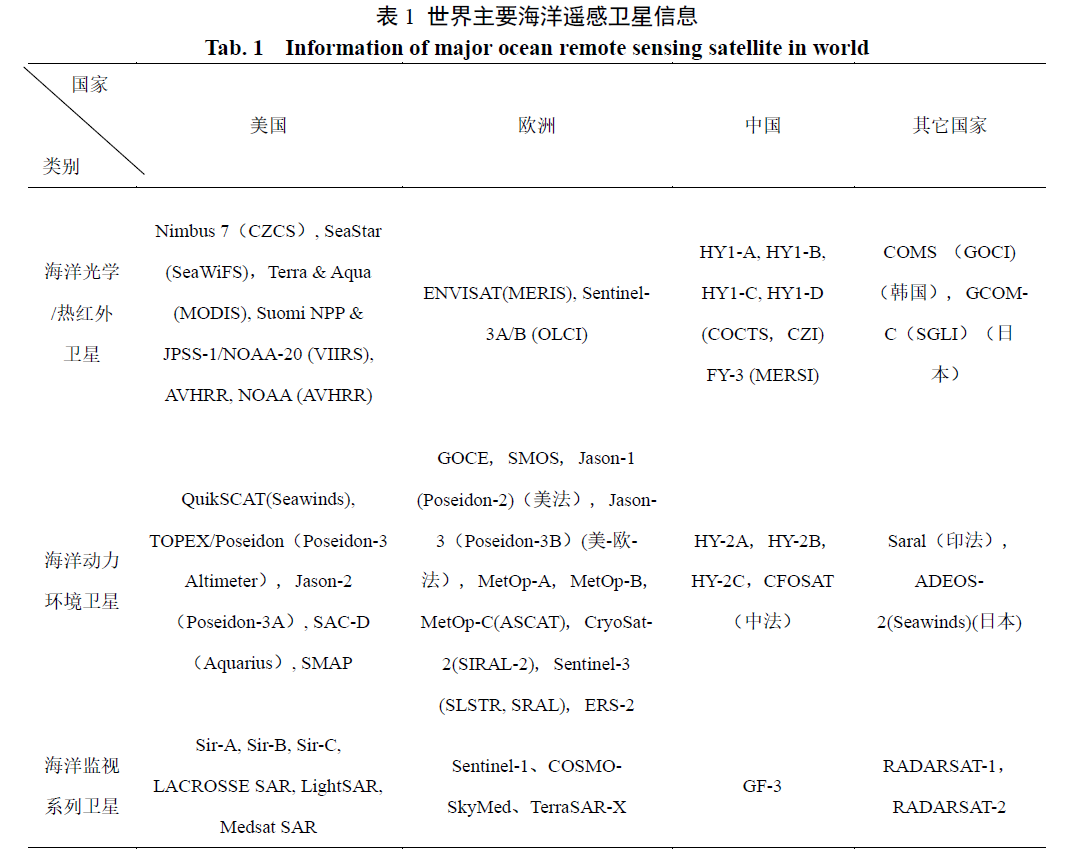
海洋动力环境卫星包括海洋2号系列卫星、中法海洋卫星与海风海浪卫星和海洋盐度卫星。海洋2号系列卫星:海洋2号系列卫星以海面风场、高度、温度等动力环境要素为探测对象。2025年前的发展包括3个阶段:第一阶段:海洋2A卫星;第二阶段:海洋2B/C/D卫星;第三阶段:新一代海洋动力环境卫星。中法海洋卫星与海风海浪卫星:中法海洋卫星(CFOSAT,China-France Oceanographic Satellite)于2009年立项,2018年10月29日在酒泉卫星发射中心成功发射(王丽丽等,2018)。航天科技集团东方红卫星有限公司负责卫星平台研制,有效载荷包括法国CNES研制的海洋波谱仪(SWIM)和中国科学院国家空间科学中心研制的微波散射计(SCAT),较HY-2B/C/D星具有更高的空间分辨率和风向精度(Lin等,2011,2019;Xu等2019;Liu等,2020)。海风海浪卫星是中法海洋卫星的后续星。国家卫星海洋应用中心于2017年底启动了该星立项论证工作。海洋盐度卫星:海洋盐度卫星列入国家空间基础设施“十二五”科研星计划,于2015年开展先期攻关,目前已经批准立项。该星载荷包括二维综合孔径海洋盐度计和多频主被动微波成像仪,分别由航天科技集团西安分院和中国科学院国家空间科学中心牵头论证。
海洋监视监测卫星将包括低轨SAR卫星、高轨SAR卫星和高轨海洋卫星,通过高分辨率成像观测实现对海洋的综合监测监视。低轨SAR卫星(高分3号卫星)于2016年(杨劲松等,2017)发射。高轨SAR卫星列入国家民用空间基础设施“十二五”科研星计划,于2015年启动先期攻关。高轨海洋卫星列入国家民用空间基础设施“十四五”科研星计划,是国内首次在静止轨道上开展海洋水色观测,并以紫外成像为手段开展溢油观测,可以得到高时间分辨率的海洋环境光学观测数据,对海洋、环境等学科和应用有重要意义。
目前国内发射的光学卫星,如高分(程益锋等,2018)系列卫星(GF-1,GF-2,GF-4)、资源系列卫星(ZY-3)、环境系列卫星(HJ-1A/B)也用于海岸带海岛的研究中。
我国海洋水色、海洋动力环境卫星数据由国家卫星海洋中心负责接收和处理;海洋监视监测SAR卫星数据由中国资源卫星中心、中科院相关研究所负责。海洋卫星数据处理主要由国家卫星海洋应用中心负责,中科院主要是作为有效载荷研制负责单位参与部分数据产品处理算法研究和软件研制工作。海洋卫星数据产品的开发由国家卫星海洋应用中心负责,并负责数据分发。目前国内海洋卫星已经初步形成了多样的海洋卫星数据产品,并由国家卫星海洋应用中心统一分发(https://osdds.nsoas.org.cn/)。 初步形成了稳定、可靠的海洋卫星数据服务体系,但海洋卫星数据的数据质量、数据分发系统能力尚需要改进和提高。
通过对近年来报告的分析,我国海洋卫星数据应用与海洋卫星的能力相比有很大的提升空间。国外对于我国海洋卫星给予很大关注,特别是HY-2A/2B卫星得到国外的重视,法国、欧洲气象卫星组织(EUMETSAT)都通过双边合作获得HY-2A/2B(雷达高度计、微波散射计)数据,并开展了应用试验,取得了较好的效果,也验证了卫星载荷的性能(张有广等,2018)。但这些应用主要是获取部分低级产品数据进行处理生成高级试验产品进行试验。例如对海洋1C的CZI载荷在浑浊二类水体和清洁水体的不同带外响应(Out-Of-Band Response)特性进行评估(Cui et al., 2018);利用海洋光学浮标(Marine Optical Buoy, MOBY)和MODIS/Terra观测的气溶胶信息对海洋1C的COCTS载荷进行辐射定标(Song et al., 2019);对于利用海洋卫星数据开展的科学研究,对数据的要求更强调定量化、易获取和质量保证,并具有一定时长的数据积累,我国海洋卫星数据在这几个方面相对国外数据还有一定的差距,所以在科学研究方面国产卫星数据的应用受到一定限制。国产海洋卫星数据整体应用不多,其主要原因在于以下几个方面:
(1)国产海洋卫星数据时间较短。国产卫星起步较晚,早前卫星数据的精度不够,很难形成业务化应用产品,近年来卫星数据质量明显提高,但时间长度不够,对于需要较长时间序列分析的研究和应用,国产卫星数据时间长度不够。
(2)国产海洋卫星数据产品需要进一步丰富。目前共享的国产卫星数据产品最高级别为2级产品。并没有可以直接用于业务化分析的三级和四级产品,对于没有任何卫星遥感知识的科研工作者和业务化应用这存在一定的困难。
(3)国产海洋卫星的推广不够。目前国产海洋卫星的分发机构较少,数据主要由国家卫星海洋应用中心分发,尚未在国内其它数据共享系统中进行共享分发。
(4)国内海洋卫星全球近实时的观测处理和数据发布(时效性)能力尚未形成,是制约数据应用的重要因素之一。
经初步调研,我国海洋科学家使用海洋卫星数据的学科领域主要集中在物理海洋学、海洋遥感、地球物理学、应用海洋学、地图学与地理信息系统等,海洋卫星数据多用于海洋数值模拟、海洋环流与涡旋、海洋内波(孙丽娜等,2018)、海洋防灾减灾(贾永君等,2018)、气候与环境变化(丁庆霞等,2016)、北极海冰(马雪沂等,2019)等科学研究。目前卫星资料使用主要以国外资料偏多。
海温数据主要来源于AVHRR、MODIS、TRMM、AMSR等卫星;多用于海气数值预报与数值同化、海洋三维温盐场实时重构、群发性海洋灾害致灾机理、黑潮入侵、海洋内波、多尺度海气相互作用及气候变化、生态过程与物理过程相互作用、北极海冰等研究。数据产品的空间精度一般在1/12°到1/4°。风场数据主要来源于QuikSCAT、ASCAT;多用于多尺度海气相互作用及气候变化、海洋环流与涡旋、台风对海洋(生态)环境影响、海洋灾害致灾机理等研究,空间分辨率通常在25km左右。海面高度数据主要来源于AVISO高度计合成产品及融合资料,GRACE和CHAMP重力资料,空间分辨率在1/4°左右;多用于数值预报与资料同化、多尺度海气相互作用与气候变暖、海洋环流与涡旋、海洋环境场实时重构、大地水准面和重力异常、地球表面流体质量多时空尺度变化及全球水质量分布研究。海面盐度数据主要来源于SMOS,Aquarius,空间分辨率在1°左右。多用于数值预报与资料同化、多尺度海气相互作用与气候变暖、海洋环流与涡旋、海洋热通量估算、海洋热盐环流等研究。叶绿素数据主要来源于MODIS、VIIRS、MERIS、SeaWiFS及Sentinel-3等,分辨率在300m-1000m之间。多用于海洋监测与防灾减灾、海洋初级生产力等研究。海面降雨数据主要来源于TRMM、AMSR-E、AMSR-2等。多用与海洋降水、海气通量、海洋气候等研究。
海洋科学部分研究尚需要更高精度卫星数据,如高分辨率海洋水色卫星,分辨率不低于30米,波段配置信噪比等不差于SeaWiFS,用于近岸河口水质监测;高分辨率海面高度数据(空间分辨率到公里级别)或海洋流场数据,用于研究海洋小尺度过程,如规划中的SWOT卫星(徐永生等,2017);高空间分辨率卫星,包括米级和亚米级的光学、微波卫星,用于海岸带、海岛变迁等监测研究,如高分2号卫星;高分辨率海洋盐度卫星(张庆君等,2017),比SMOS,Aquarius卫星的分辨率高,且受干扰少;覆盖西太平洋海域(特别是130°E以东)的实时或准实时通信卫星。其他如对静止轨道卫星的需求,用于中国近岸水体水质监测。同时,在辨识海洋涡旋研究中,亟需SAR卫星图像。
通过国家民用空间基础设施建设,我国正逐步建立较为完备的海洋卫星观测系统。目前海洋卫星数据的下载和使用已经没有问题。但由于我国海洋卫星发展较晚,时间长度不够,再加上科学研究长期以来一直使用国外数据,改变这种沿用国外卫星数据的习惯还需要一定时间,国产海洋卫星数据推广应用还需要进一步提升。
我国海洋卫星起步较晚,早前的卫星与有效载荷性能和国际先进水平有一定差距。HY-1A卫星在轨时间短,HY-1B卫星有效载荷存在太阳照射污染观测数据存在问题,实际上不具备提供有效数据支持的能力。2018年成功发射的HY-1C(林明森等,2019)光学卫星和2019年发射的HY-1D卫星已经达到国外同类卫星产品水平,但目前卫星在轨工作时间只有两年多,数据的时间长度较短,同时由于科研和业务工作者长期使用国外数据形成一定的惯性,国产海洋卫星数据的推广使用还需要一定的时间。
目前海洋卫星数据的分发已经有了明显的提升,国家卫星海洋应用中心已经通过中国海洋卫星数据服务系统将卫星数据进行了全面的共享(osdds.nsoas.org.cn)。但数据质量尤其是二级以上产品质量的改善需要广大用户的测试和反馈。数据用户,特别是具有研究能力的研究团队需要对数据处理过程有完整的掌握,发现问题并提出改善数据质量的办法,从而参与数据的开发和利用,如NASA的水色数据产品,其数据参数和处理过程都集中在共享软件SeaDAS中,用户较容易掌握,而目前海洋卫星有共享相关的数据使用手册,但在数据处理及使用说明等方面还有待加强。另一方面,在部分研究领域,缺少相关数据支持,如在海冰研究领域,国内缺乏专门的数据或相关已处理并公开的成;SAR卫星数据经常处于购买状态,如发生重大事故,无法获取第一手卫星资料,同时缺少遥感影像使用;缺乏准实时业务化的多源卫星融合产品。
重工程实现、轻数据处理与应用是我国遥感卫星规划和实施中普遍存在的现象,在我国海洋卫星计划在实施中对于数据处理、反演模型优化、试验验证、地面和在轨标定等工作投入明显不足,处理技术研究组织的明显不足,导致数据定量化与稳定性不足,数据质量还有待提高。相关部门目前对于数据应用能力的提升关注不够,缺乏长时间序列、高质量、易于使用的卫星数据产品,被使用频率较低。
海洋卫星数据在海洋科学研究中具有重要的意义,获得长期稳定可靠的卫星数据产品是海洋科学研究对卫星数据产品的需求。充分利用好国际和国内海洋卫星资源,将对提升我国海洋科学研究水平发挥积极的作用。
进一步加强我国海洋卫星数据资源的利用研究,加强科学卫星与业务卫星方面的协调和配合机制,加强海洋科学家和卫星研制、数据应用方面的交流。针对全球海洋水色的观测、全球海面高度、中国近海海岸带生态环境监测、关键海区目标的探测、海岛调查等重要科学问题,制定我国海洋卫星的长期发展规划,以便于获得长期稳定可靠卫星数据产品。
海洋卫星的数据定标和处理是后续卫星数据应用的保障。加强海洋卫星数据的处理是目前苛待解决的重要问题。呼吁增加海洋卫星数据的后续处理力量,应针对不同应用的系列卫星,成立稳定的海洋卫星数据处理、分发及技术支持队伍,这将为海洋卫星数据质量的改进提供支撑和保障,是产出稳定高质量的海洋卫星数据产品的基础。
卫星数据是国家的宝贵财富,制定良好的共享机制,是推广使用国产卫星数据的必要条件。建议不仅仅将卫星数据本身,同时应该将数据处理方法/算法写入数据手册并全面开放共享,以便数据的推广和深入应用。同时建议将海洋卫星数据产品在国家海洋科学数据中心、国家地球系统科学数据中心、国家对地观测科学数据中心等多个科学数据平台进行全面的推广使用。
文质彬,吴园涛,李琛,殷建平. 我国海洋卫星数据应用发展现状与思考[J]. 热带海洋学报, 2021: 0–0. DOI:10.11978/2020122.
http://journal15.magtechjournal.com/Jwk3_rdhyxb/CN/10.11978/2020122
以中国知网1972~2020年间的北大核心期刊《海洋通报》文献记录为研究对象,运用文献计量分析方法可视化分析《海洋通报》所发表论文的研究内容及其演变。
文献计量学是利用数学和统计学方法定量分析科技文献外部表征,进而揭示学术研究活动特征,已广泛地应用于多学科领域的发展现状和规律探索。文献计量学可以用于期刊评价,例如核心期刊的遴选,也可以从宏观角度揭示某一种学科的发展规律,并在微观角度揭示学科的知识流动。
本文将使用文献计量方式分析《海洋通报》历年发文情况,制作关键词、作者、机构等知识共现谱图,通过共现聚类使主要研究内容、人员、机构的分布和关联清晰展现。因为受知识水平限制,本文不做过多的微观解释分析,主要以知识图谱展示,从宏观角度展现《海洋通报》。
《海洋通报》前身为《海洋科技资料》,1982年改现用名《海洋通报》,中国工程院院士方国洪担任主编,由自然资源部主管,国家海洋信息中心和中国海洋学会主办,自然资源部北海局、东海局和南海局协办,是国内海洋领域具有较大影响的综合学术刊物之一。双月刊 (CN 12-1076/P,ISSN 1001-6392),大16开本,120页,逢双月 15 日出版,国内外公开发行。主旨为:坚持科学技术面向经济建设的方针,反映现代海洋科技发展的方向与水平,推广科技成果,传播科技信息,团结广大海洋科技工作者,积极开展学术交流,为繁荣我国的海洋事业服务。设有论文与综述等栏目。主要报道内容包括海洋水文、气象、物理、化学、生物、地质等基础理论研究和应用研究,以及海洋通报、资源开发、水产养殖、环境保护、环境预报、仪器设备等方面调查、研究和管理的新发展、新理论、新观点、新方法、新经验。它集学术性与技术性于一体,适合于广大海洋科技工作者、管理人员和有关大专院校的师生阅读。
由于《海洋通报》曾用名《海洋科技资料》,因此中国知网检索:
检索条件: ( 拼音刊名= CJFD_HUTB or 出版物代码= CJFD_HUTB );检索范围:总库。
此处,一般应剔除卷首语、编辑部声明等文献,进而得到纯粹的科学研究文献。
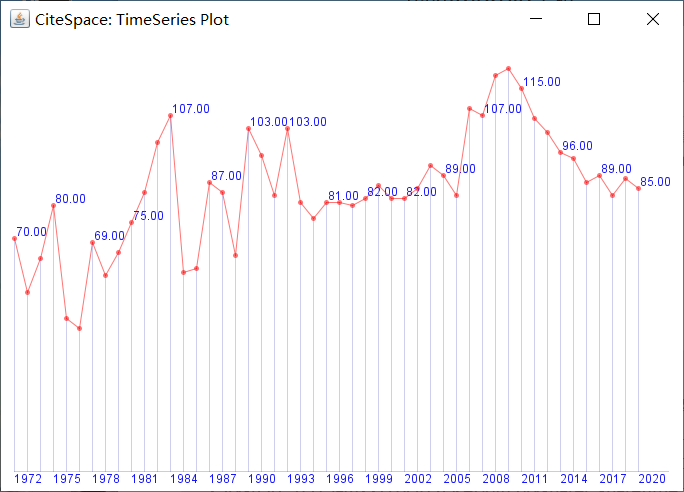
1972-2020年共发表4110篇文章,年发文一般不超过120篇,发文量在同类期刊属于中游水平。
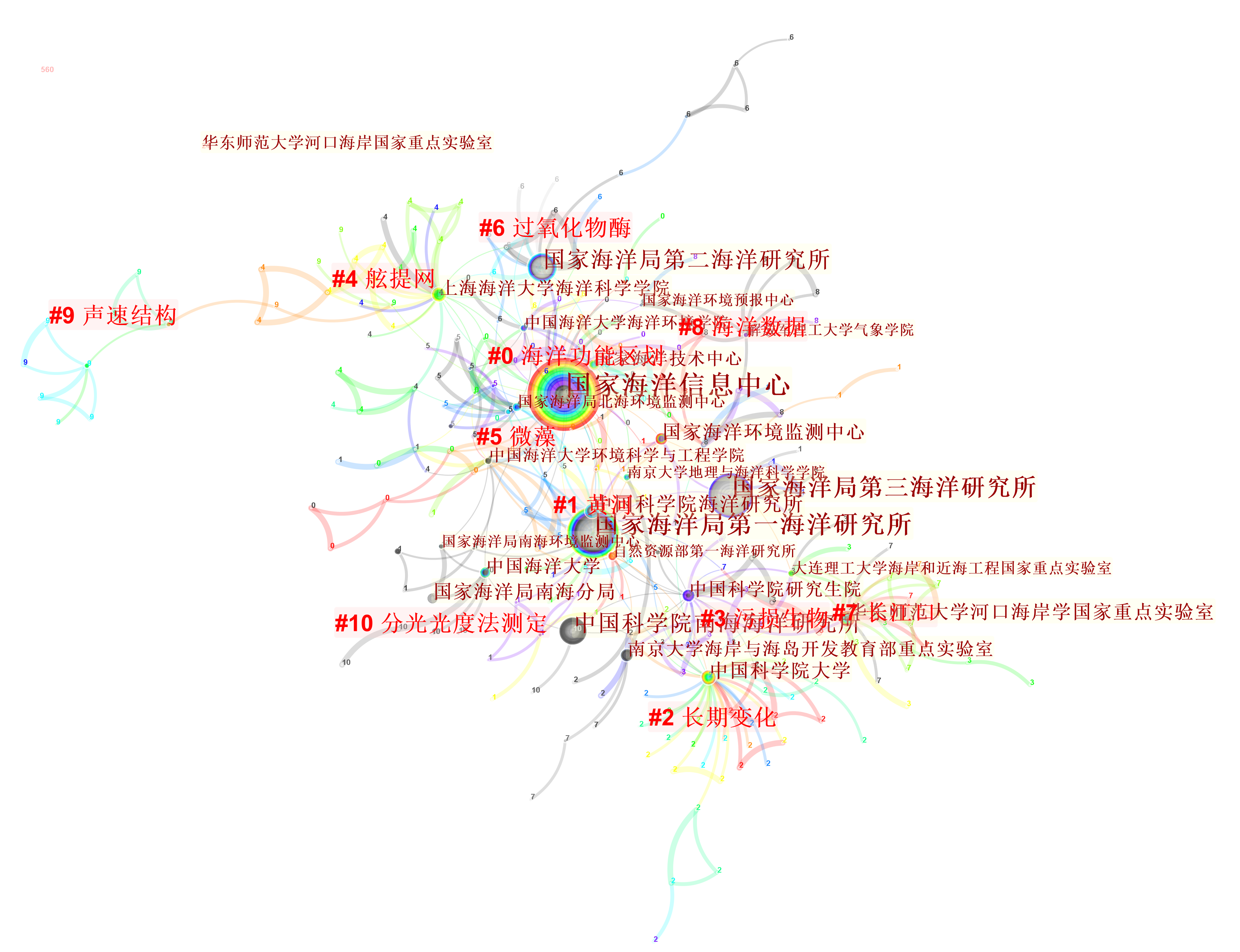
本图展现的机构节点数共计1081个(按照一定的节点强度阈值展现,表示研究单位数,并非全部),共现连接线477(表示合作关系),各单位之间合作关系相对上一篇《海洋科学进展》所得结论(比例接近1:1)偏弱。
发文最多的单位为国家海洋信息中心,表现在图谱上的特点就是节点中心性强,节点圈大(最大的圈),其文献的节点数超过167。其次为海洋一所,其文献的节点数为114,第一和第二之间的发文数量差距不太大。
图中的节点(圆圈)的颜色表示时间,灰色表示年代久远的文献,彩虹色表示为近几年的文献。比如海洋三所多为为灰色,表示其文献的历史较早,目前活跃度不高。

这张图表明《海洋通报》文章的主要关注点是浮游植物、沉积物分布、数值模拟、政府间海洋学委员会、大气环流、加里曼丹、黄河口、水下实验室、沿海国等,和其他学术期刊不同的是,《海洋通报》形成了沿海国、加里曼丹、政府间**等国际热点聚类文献簇,以及海洋经济文献簇,可见,《海洋通报》发文除了形成海洋科学、海洋调查等文献聚类簇,也形成了一些软课题文献聚类簇。这也是和其他学术期刊的显著区别之一。
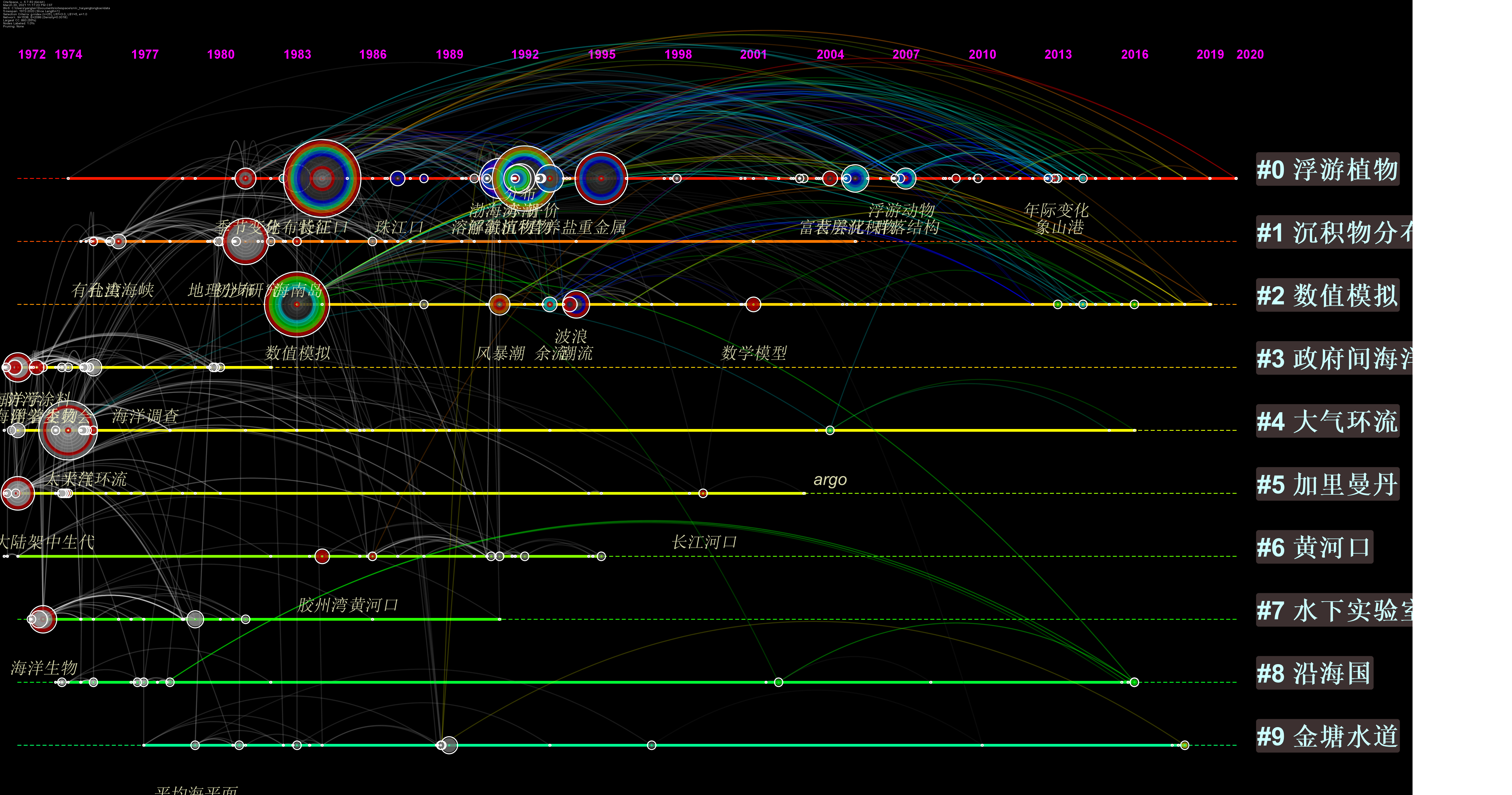
这张时间图谱中不同聚类由平行轴线代表,不同关键词频次由节点大小代表,关键词首次出现年份由位置代,水平线的虚实表示其持续性,#前面的数字表示聚类的强度,0表示最强的聚类簇。从中可以基本判断,浮游植物持久性最强,说明热度持续,节点连线最为丰富,表明知识流动性好。
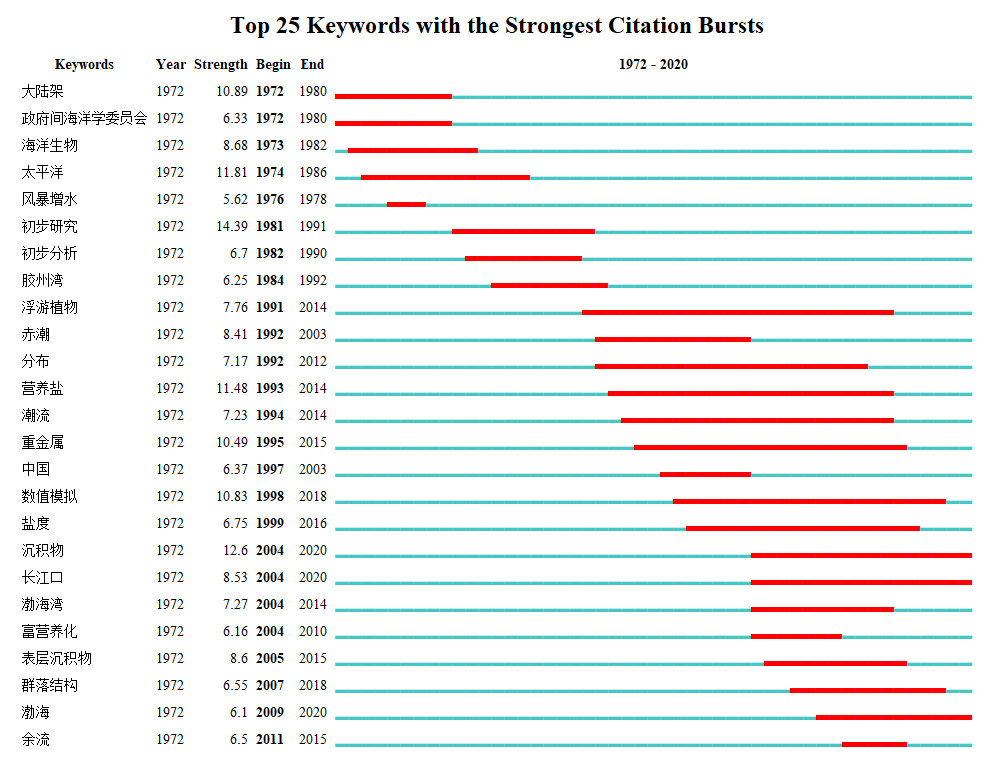
突现(Burst)是指特定时间段内通过关键词频次的变化将频次高的词探测出来,在一定程度上反映《海洋通报》的研究趋势。与上一幅时间轴的展示相差不多,但此处更加清晰的展现整体发文趋势,然而仅余流为近十年的一个突现词,可见《海洋通报》的热点突现并不明显。
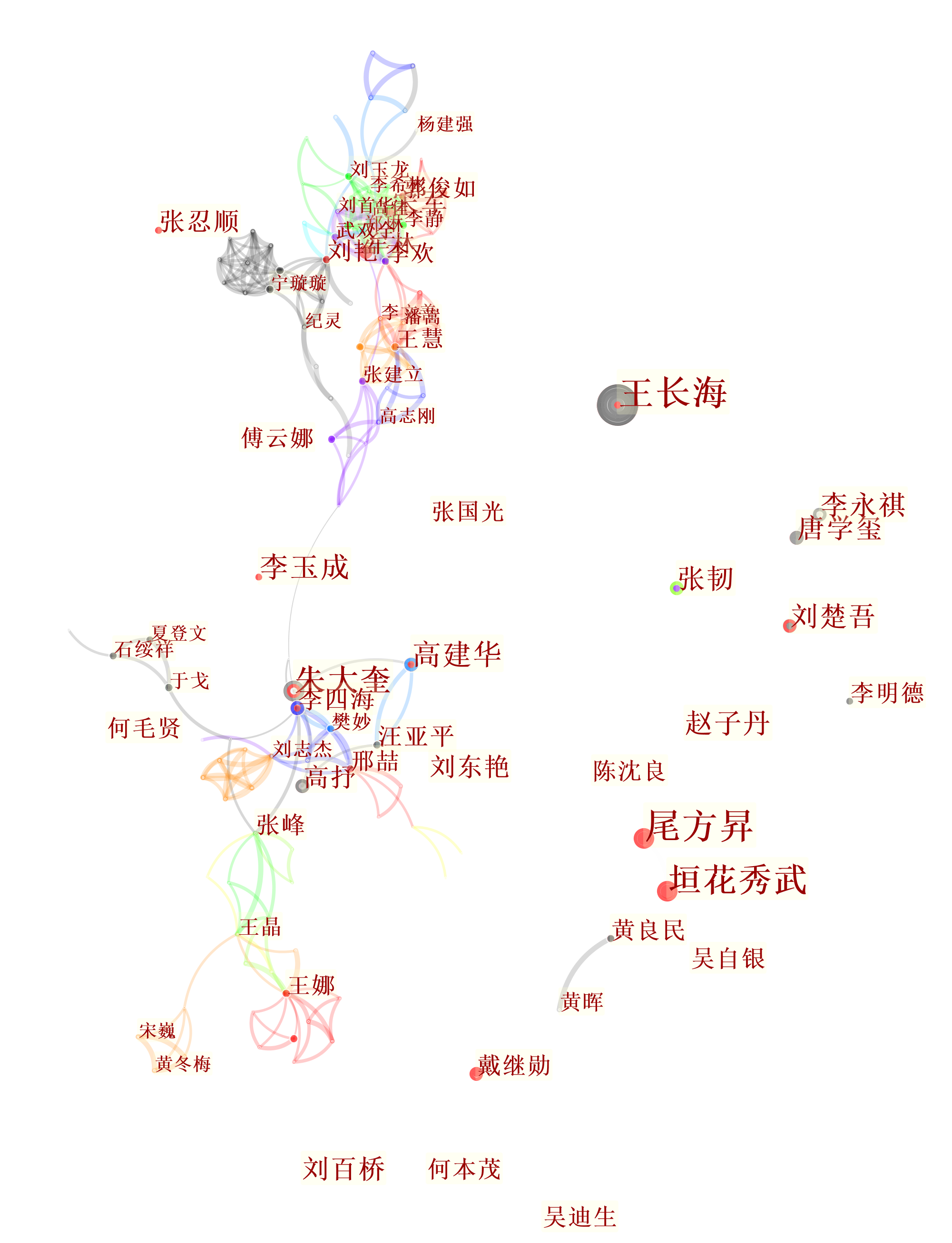
《海洋通报》发文作者合作脉络极为特别,聚类之后形成了奇特的长条形,说明作者合作关系扁平化,单独的研究群体内部合作良好,但研究群体之间缺乏深度合作,这和《海洋科学进展》、《海洋技术学报》等期刊的作者群落(发散合作,交叉性强)明显不同。此外,还有大批作者由于节点的强度不足,而游离在长条之外,其背后的原因尚待分析。
图谱颜色的含义为,彩色表示时代较近,灰色表示时代较久。节点大小和位置表示作者的发文频次和中心性。连接线粗细表示不同作者之间的合作强度。
网络中节点的
中心性测量的是网络中节点的位置重要性。有两类节点可能具有较高的中介中心性:1)与其他节点高度相连的枢纽节点;2)位于不同聚类之间的节点。
图谱中所展现的作者是按照一定的权重提取的,属于共现性强的作者。这里的节点数据并非全部作者,上面的关键词和机构也是如此。全部作者、机构和关键词的节点数据非常庞大,然而按照权重(具体为g-index)提取的节点更具代表性。
遗憾的是,CNKI导出的数据不含有引用信息,因此无法通过程序进行文献共引的计量分析,而文献的引用关系最能代表知识的流动脉络。这里,仅列举利用CNKI数据库检索到引用次数最多的前10个文献:
[1]王晓坤,马家海,叶道才,陈孝德.浒苔(Enteromorpha prolifera)生活史的初步研究[J].海洋通报,2007(05):112-116.
[2]许妍,梁斌,鲍晨光,兰冬东,于春艳,马明辉.渤海生态红线划定的指标体系与技术方法研究[J].海洋通报,2013,32(04):361-367.
[3]王建伟,阎斌伦,林阿朋,胡静平,沈颂东.浒苔(Enteromorpha prolifera)生长及孢子释放的生态因子研究[J].海洋通报,2007(02):60-65.
[4]王金辉,黄秀清,刘阿成,张有份.长江口及邻近水域的生物多样性变化趋势分析[J].海洋通报,2004(01):32-39.
[5]彭云辉,孙丽华,陈浩如,王肇鼎.大亚湾海区营养盐的变化及富营养化研究[J].海洋通报,2002(03):44-49.
[6]李加林,杨晓平,童亿勤,张殿发,沈永明,张忍顺.互花米草入侵对潮滩生态系统服务功能的影响及其管理[J].海洋通报,2005(05):33-38.
[7]杨建强,崔文林,张洪亮,徐子钧.莱州湾西部海域海洋生态系统健康评价的结构功能指标法[J].海洋通报,2003(05):58-63.
[8]赵焕庭,王丽荣.中国海岸湿地的类型[J].海洋通报,2000(06):72-82.
[9]沈焕庭,朱建荣.论我国海岸带陆海相互作用研究[J].海洋通报,1999(06):11-17.
[10]周洪军,何广顺,王晓惠,李长如,杨娜.我国海洋产业结构分析及产业优化对策[J].海洋通报,2005(02):46-51.
截止本文发布,《海洋通报》被引用最多的文献为王晓坤等发表于2007年的浒苔(Enteromorpha prolifera)生活史的初步研究,次数为172次,其次为许妍等人2013年发表的渤海生态红线划定的指标体系与技术方法研究,被引199次。
此外CNKI可以统计文献下载次数,下载频次可反映文献受关注的程度,期刊最高下载量的两篇论文为2500左右,稍显偏低。
通过对核心期刊《海洋通报》1972~2020年的文献计量分析,从期刊引文、关键词突现和研究热点时序聚类分析发现:《海洋通报》所刊论文的主要研究方向不仅涉及海洋科学技术,还涉及如海洋经济、沿海国等领域的研究;期刊最显著的特色是作者的合作脉络呈现扁平化,不发散。初步分析,原因极可能为海洋信息数据的不流通限制了作者合作的范围,这是目前海洋科学研究领域的极大弊端。
众所周知,国家海洋信息中心负责我国海洋调查观测数据的集中管理和数据共享,其数据黑洞的大名也由来已久,且至今难以改变。《海洋通报》为其主办的学术期刊,信息中心在该期刊的发文比例最大,造成其文献的影响强度也最高,而海洋信息数据的不共享或者有限共享导致作者的合作研究受到局限,最终表现在图谱上文献作者的扁平化合作关系,可以理解为利用近乎垄断的数据资源,在一批国家海洋信息中心的作者之间形成了扁平合作关系,其内部的交叉合作也非常薄弱。
目前海洋科学数据的供给侧严重失衡,需求和供给明显的失衡,海洋科技工作者对海洋数据的迫切需求和海洋数据的供给不足形成当下海洋科学研究的卡脖子因素,严重制约了海洋领域的科学技术发展。数据黑洞还进一步造成了数据调查的重复性,浪费了大量国家资源。可以说数据的难共享百害无一利。
实现数据共享的道路还很长,一些障碍还比较根深蒂固,比如保密这个大帽子,然而实际上无一部法律规定明确说海洋信息数据(如海洋站潮汐观测数据)是涉及国家安全不得共享。数据供给的改革还联系到部门利益,打破数据垄断,释放数据活力,需要壮士断腕般的魄力。然而一旦实现数据共享,其增值必将远大于目前有限范围内数据使用者所创造的价值。
比如一位申请者在申请月均潮汐数据用于海平面研究时的申请受挫,对方的惯用理由即为保密:
下一步,全国海洋科技工作者团结起来,深入领会习近平总书记海洋命运共同体论述,实现海洋数据共享,建设海洋强国,为增进人类海洋福祉不懈努力。
小编也将进一步搜集整理广大海洋科技工作者数据申请的被拒案例(若有诉求,可本公众号后台留言,小编将整理成集),进行广泛的数据共享满意度调查,适时地向主管部门进行情况反映,从需求侧倒闭供给问题难的解决方案。
文献总数:4953 篇; 检索条件: ( ( ( 拼音刊名= CJFD_HYFZ or 出版物代码= CJFD_HYFZ ) NOT ( 作者=’编辑部’ or 中英文作者=’编辑部’ or 作者名称=’编辑部’ ) ) NOT ( 主题%=’研讨会’ or 题名%=’研讨会’ ) );检索范围:中文文献。
主管:中国科学技术协会
主办:中国海洋湖沼学会
承办:中国科学院海洋研究所
主编:孙松 研究员
创刊:1957年 刊期:双月刊
《海洋与湖沼》是中国水科学领域最早最有影响力的综合性学术刊物之一。期刊以报道基础和应用基础研究成果为主,重点刊载有影响的重要技术研发成果论文。内容涉及广泛,主要发表江河湖海、沼泽湿地等方面的高端科技论文,学科涵盖生物、物理、化学、地质等多个学科及其分支,形式有研究论文、研究简报、高新技术、高水平综述、学术争鸣等。
《海洋与湖沼》在国际国内水科学领域具有广泛影响。现已收录本刊的国外重要数据库有:CA(美国《化学文摘》)、SA(英国《科学文摘》)、JICT(日本《科学技术文献速报》)、РЖ(AJA) (俄罗斯《文摘杂志》等;国内收录本刊的重要数据库有:中国科技论文引文统计分析数据库、中国科学引文索引数据库、中国期刊全文数据库等。
据中国科学技术信息研究所发布的《中国科技期刊引证报告》(核心版)期刊检索统计结果表明,近十几年来(1996—2012)《海洋与湖沼》的总被引频次居国内水科学领域期刊首位,影响因子及总分排名均居于前列。
GMT的动画功能是版本6之后新增加的,主要是调用movie程序,隐藏中间过程,直接制作gif图或者视频。因为偏难,用的人也不多,至今movie的使用和反馈都不如其他功能。本文也仅仅以官方提供的两个例子为例,并非小编自己写的代码。自己编程写动画的话,可替代的途径是写for循环制图,然后使用GM一键制作动画。
The movie module can generate GMT animation sequences using a single-plot script that is repeated for all frames, with some variation using specific frame variables. The module simplifies (and hides) most of the steps normally needed to set up a full-blown animation job. Instead, the user can focus on composing the main frame plot and let the parallel execution of frames and assembly of images into a movie take place in the background. Individual frames are converted from PostScript plots to lossless, transparent PNG images and optionally assembled into an animation (this last step requires external tools that must be present in your path; see Technical Details below). For opaque PNG images, simply specify a background color via -G.
GMT提供了12个案例,今天用地震分布的例子简单介绍其用法。
GMT动画需要安装GraphicsMagick(图片GIF)和FFmpeg(视频),下载地址:
安装后,确保window系统path路径中已经包含上述程序,一般情况下,win和linux都可以自动添加路径,无需再操作。
先运行例1进行测试,检查是否已经具备条件。
注意,需要修改主程序中$# -eq 0为$# -eq 1,或改为任意个非0数字。
1 | if [ $# -eq 1 ]; then # Just make master PostScript frame 0 |
然后运行,期间中间会产生许多临时文件,结束后会自动删除这些文件,仅仅保留动画。结果如下:
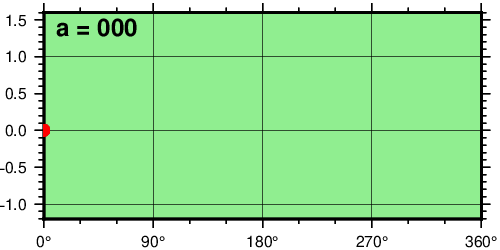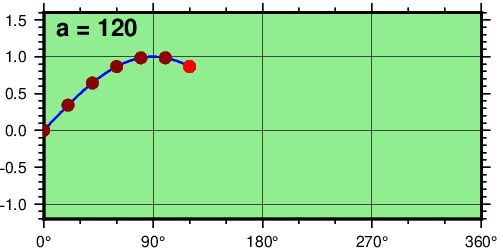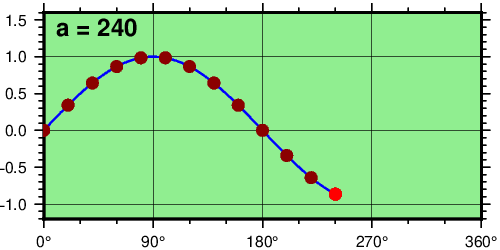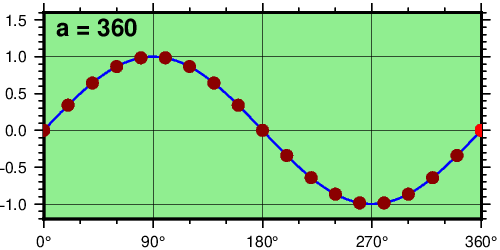
下面是例子8的代码,作者是GMT创始人Paul,同样需要注意修改0为非0。
1 | #!/usr/bin/env bash |
中间依旧产生许多文件,不需要管。最后得到的结果为: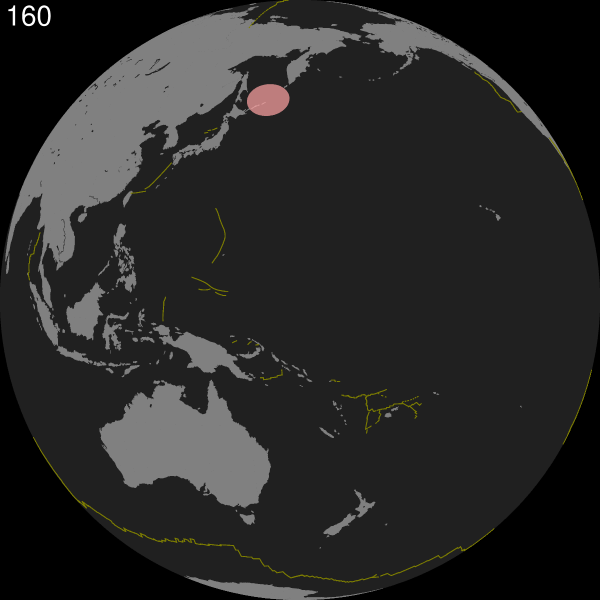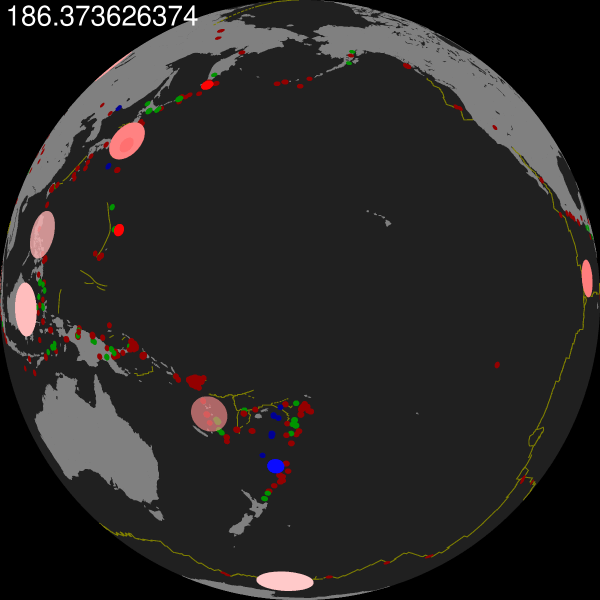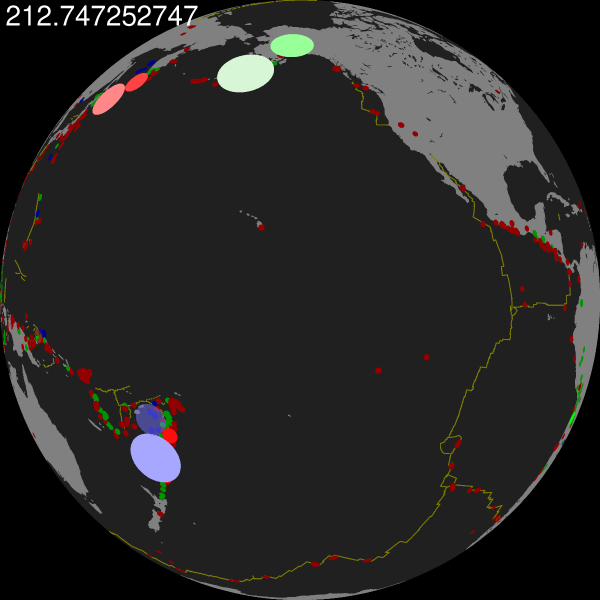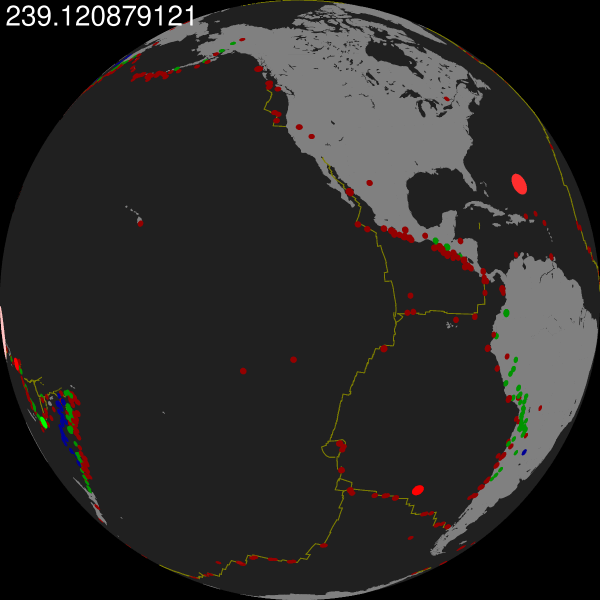
视频:
Paul还制作了一个更为复杂的动画视频,加入了地形和光照,渲染时间花费约1个小时。
The movie took ~1 hour to render on a 24-core MacPro 2013.
Waiting
GMT是绘图工具,也是数据分析工具,经过几十年的维护,计算和绘图功能都已经相对成熟。今天分享一个使用GMT进行卫星高度计交叉分析的例子,交叉点分析是卫星测高领域常用的数据质量检核手段,历史文献表明大部分的交叉点基于复杂的轨道理论,计算速度缓慢,GMT的x2sys采用了几何图形理论,计算速度快,精度高。小编已经将这个功能纳入了卫星测高GAT开源程序(尚在完善中)。
全套程序将用到:
awk预处理HY-2B数据,主要是去重和排序。1 | #!/usr/bin/env bash |
目前的bug是:
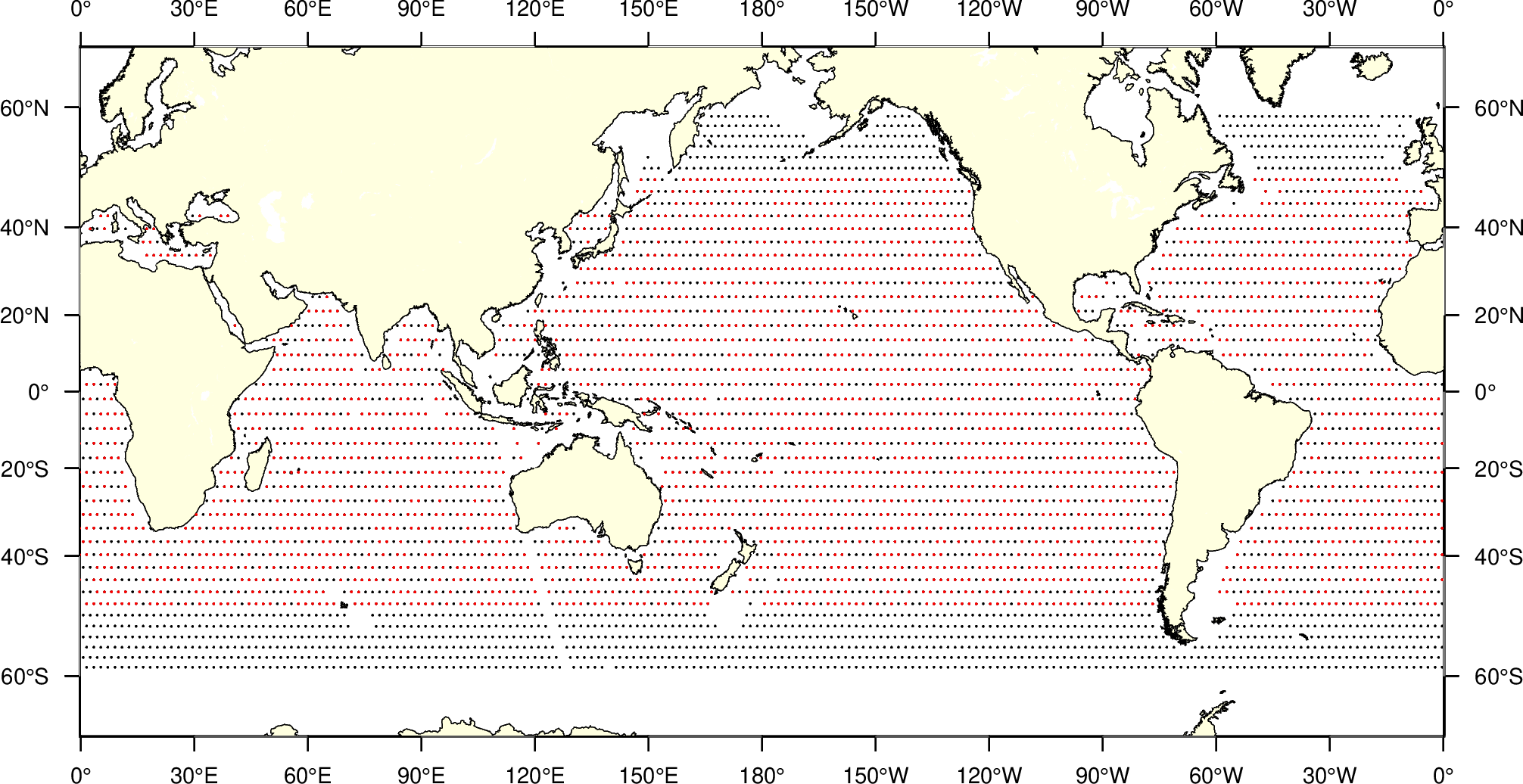
统计结果:
1 | -14.8227094512 -7.66263064551 -0.00662686124578 (均值) |
上述统计仅仅采用有限数据,不代表卫星的最终质量分析结果。
关于HY-2B的分析结果可参考下面文献:
[1] WANG J, XU H, YANG L, 等. Cross-Calibrations of the HY-2B Altimeter Using Jason-3 Satellite during the Period of 2019.4~2020.9[J/OL]. Frontiers in Earth Science, 2021, 9[2021–03–15]. https://www.frontiersin.org/articles/10.3389/feart.2021.647583/abstract. DOI:10.3389/feart.2021.647583.
[2] JIA Y, YANG J, LIN M, 等. Global Assessments of the HY-2B Measurements and Cross-Calibrations with Jason-3: 15[J]. Remote Sensing, 2020, 12(15): 2470. DOI:10.3390/rs12152470.
程序发表的相关文献:
[1] WESSEL P. Tools for analyzing intersecting tracks: The x2sys package[J]. Computers & Geosciences, 2010, 36(3): 348–354.
[2] WESSEL P. XOVER: A cross-over error detector for track data[J]. Computers & Geosciences, 1989, 15(3): 333–346.
示例数据和代码以在GitHub托管:
https://github.com/GenericAltimetryTools/CalAlti/tree/master/crossover
上两篇的研究对象是《海洋科学进展》和《海洋技术学报》,本文研究海洋领域另一份北大核心期刊《海洋工程》。海洋
科学和技术的面貌已大致呈现,本文首先展现海洋工程的研究范围,其次分析科学、技术和工程的区别和共性,是不是海洋科学技术在海洋工程中开花结果呢?
以中国知网1992~2020年间的北大核心期刊《海洋工程》文献记录为研究对象,运用文献计量分析方法可视化分析《海洋工程》所发表论文的研究内容及其演变。研究表明,《海洋工程》期刊的研究内容主要涉及海洋平台、平台动力环境分析等方面,论文主要以不同的海洋平台系统、环境影响因子组成文献簇,包含系泊系统、海洋平台、两层流体、不规则波、振动、潜水器、海底管线、吸力锚、力学模型等,发文趋势分析表明海洋工程的关注点正从传统的波浪作用向内孤立波等深层水下因子转变。研究机构以数家国家重点实验室为主,机构间合作强度偏弱。
文献计量学是利用数学和统计学方法定量分析科技文献外部表征,进而揭示学术研究活动特征,已广泛地应用于多学科领域的发展现状和规律探索。文献计量学可以用于期刊评价,例如核心期刊的遴选,也可以从宏观角度揭示某一种学科的发展规律,并在微观角度揭示学科的知识流动。
本文将使用文献计量方式分析《海洋工程》历年发文情况,制作关键词、作者、机构等知识共现谱图,通过共现聚类使主要研究内容、人员、机构的分布和关联清晰展现。因为受知识水平限制,本文不做过多的微观解释分析,主要以知识图谱展示,从宏观角度展现《海洋工程》。
《海洋工程》是由中国科学技术协会主管,中国海洋学会主办,南京水利科学研究院、上海交通大学承办的综合性学术刊物。已被美国剑桥科学文摘(CSA);联合国《水科学和渔业文摘》(ASFA);日本科学技术振兴机构中国文献数据库(JST);中国科技核心期刊(中信所);中国科技期刊精品数据库(中国知识资源总库);中国核心期刊(遴选)数据库(万方数据库);中国期刊全文数据库(CJFD);中国学术期刊综合评价数据库(CAJCED);中国科学引文数据库来源期刊(中科院文献中心);中文科技期刊数据库;中国学术期刊文摘及中国期刊网收录。主要刊载近海工程、海岸工程、水下潜水救捞技术、海洋能源利用等方面学术论文,报道科技动态,并开展问题讨论和技术交流。主要栏目有海洋工程研究、设计、试验、生产、使用、管理及学会动态。读者对象为海洋工程领域的科研教学和工程技术人员。
由于《海洋工程》无曾用名,因此中国知网检索:
JN=海洋工程
此处,一般应剔除卷首语、编辑部声明等文献,进而得到纯粹的科学研究文献。
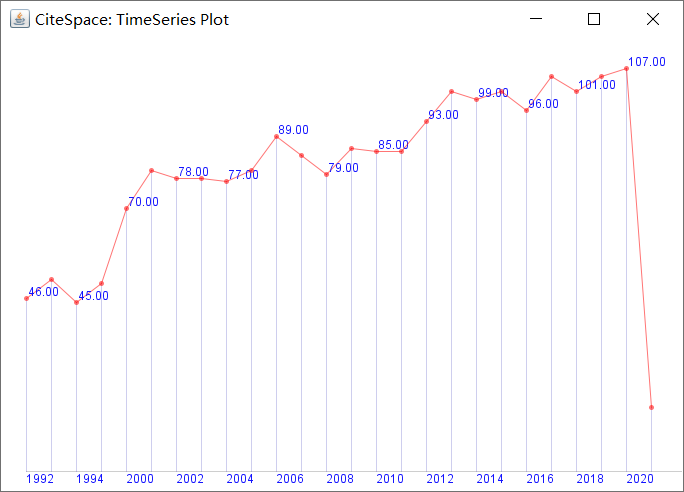
1992-2020年共发表2068篇文章,年发文一般不超过110篇,发文量在同类期刊属于中游水平。
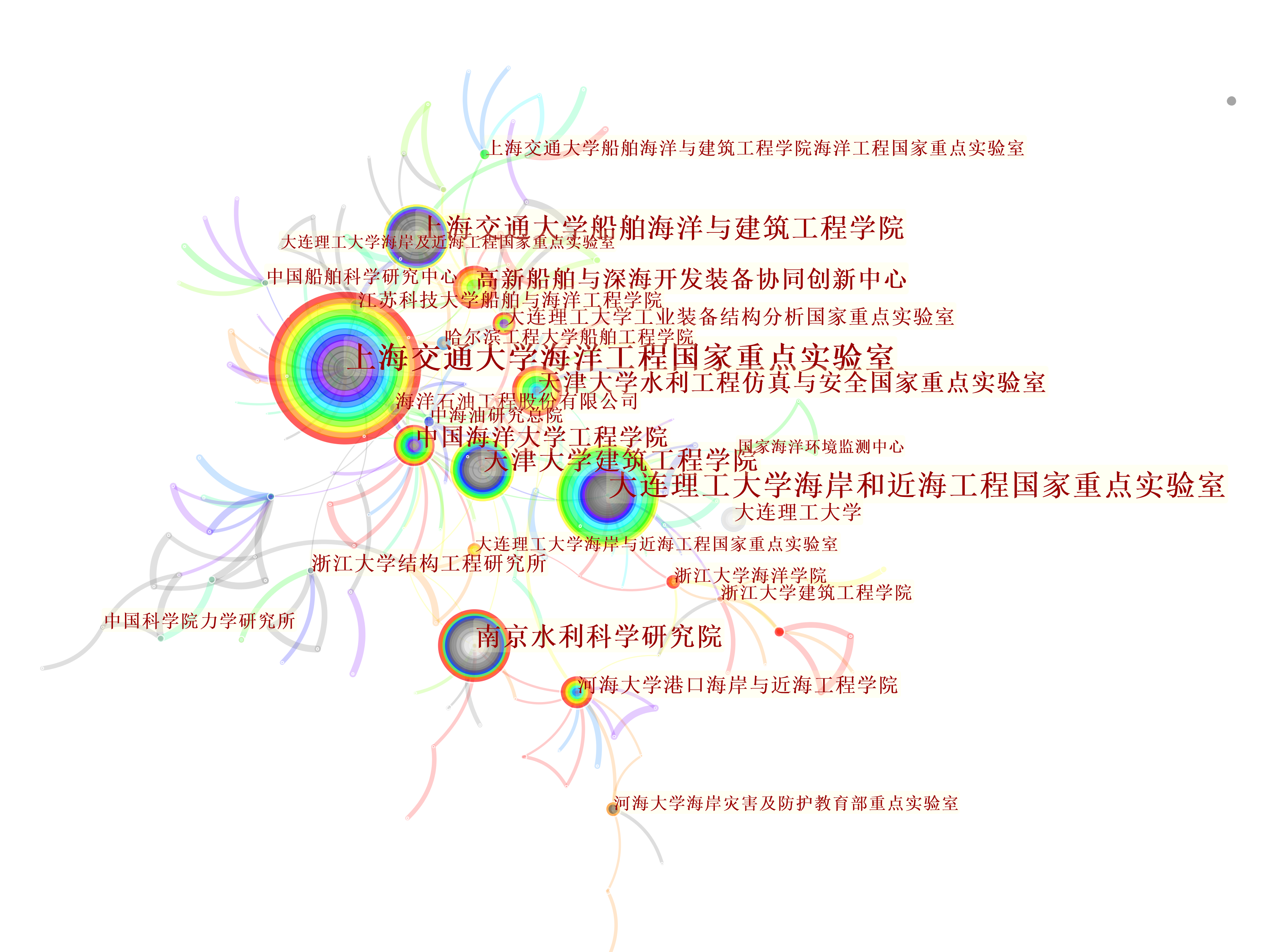
机构节点数共计611个(表示研究单位总数),共现连接线321(表示合作关系),各单位之间合作关系相对上一篇《海洋科学进展》所得结论(比例接近1:1)偏弱。
发文最多的单位为上海交通大学海洋工程国家重点实验室,表现在图谱上的特点就是节点中心性强,节点圈大(最大的圈),其文献的节点数超过149。其次为大连理工大学海岸与近海工程国家重点实验室,其文献的节点数为110,第一和第二之间的发文数量差距不大。此外海洋工程领域发文较多的还有天津大学水利工程仿真与安全国家重点实验室、大连理工大学工业装备结构分析国家重点实验室、华东师范大学河口海岸学国家重点实验室等国家重点实验室。
图中的节点(圆圈)的颜色表示时间,灰色表示年代久远的文献,彩虹色表示为近几年的文献。比如南京水利科学研究院内部为灰色,外部为较少的彩虹色,表示其文献的历史较早,目前活跃度不高,而高新船舶与深海开发装备协同创新中心主要为彩色,2016年之后才开始较多的发表海洋工程方向文章。
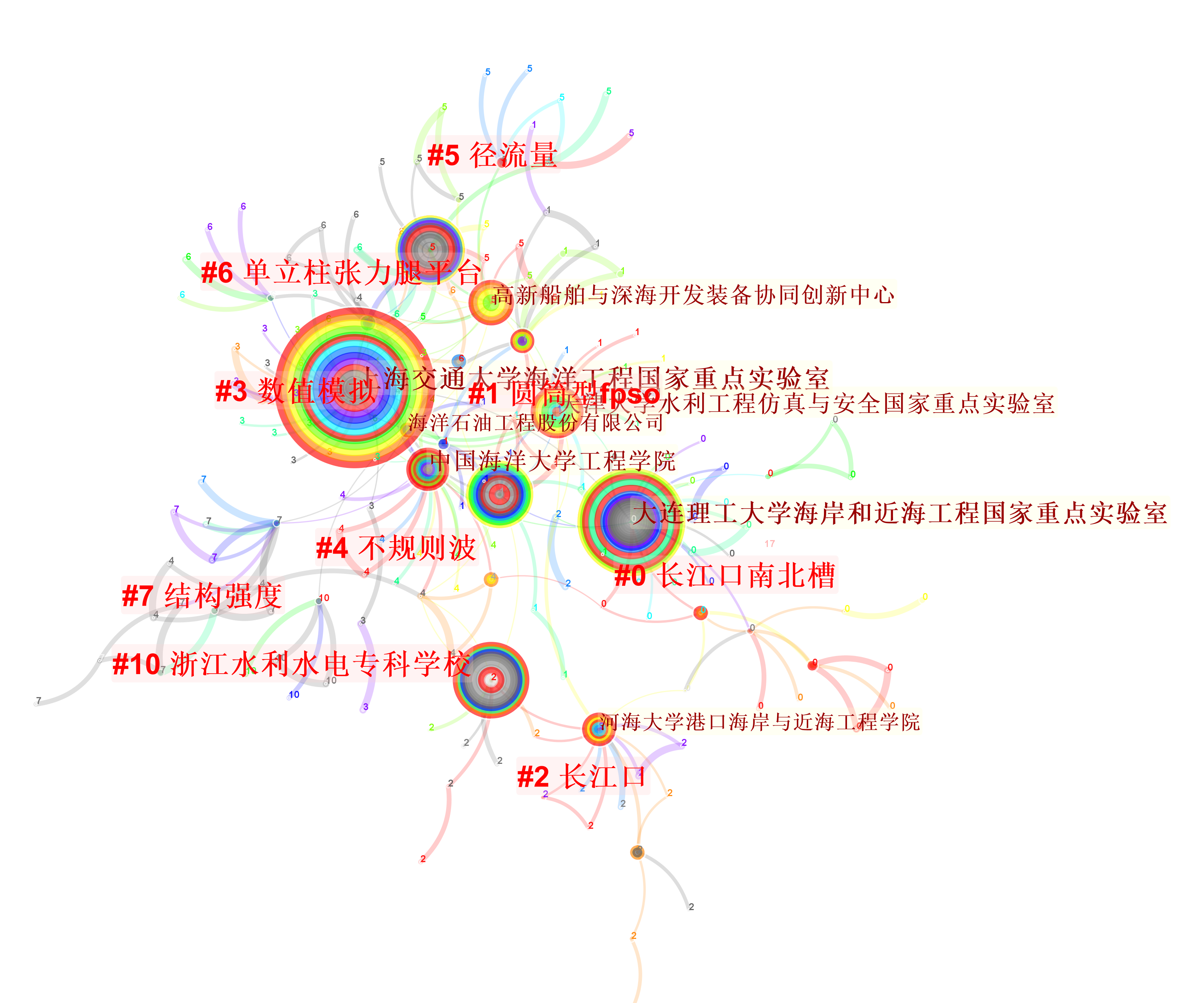
这张图展示的是研究机构和关键词的共现聚类,通俗理解为研究机构的研究兴趣。
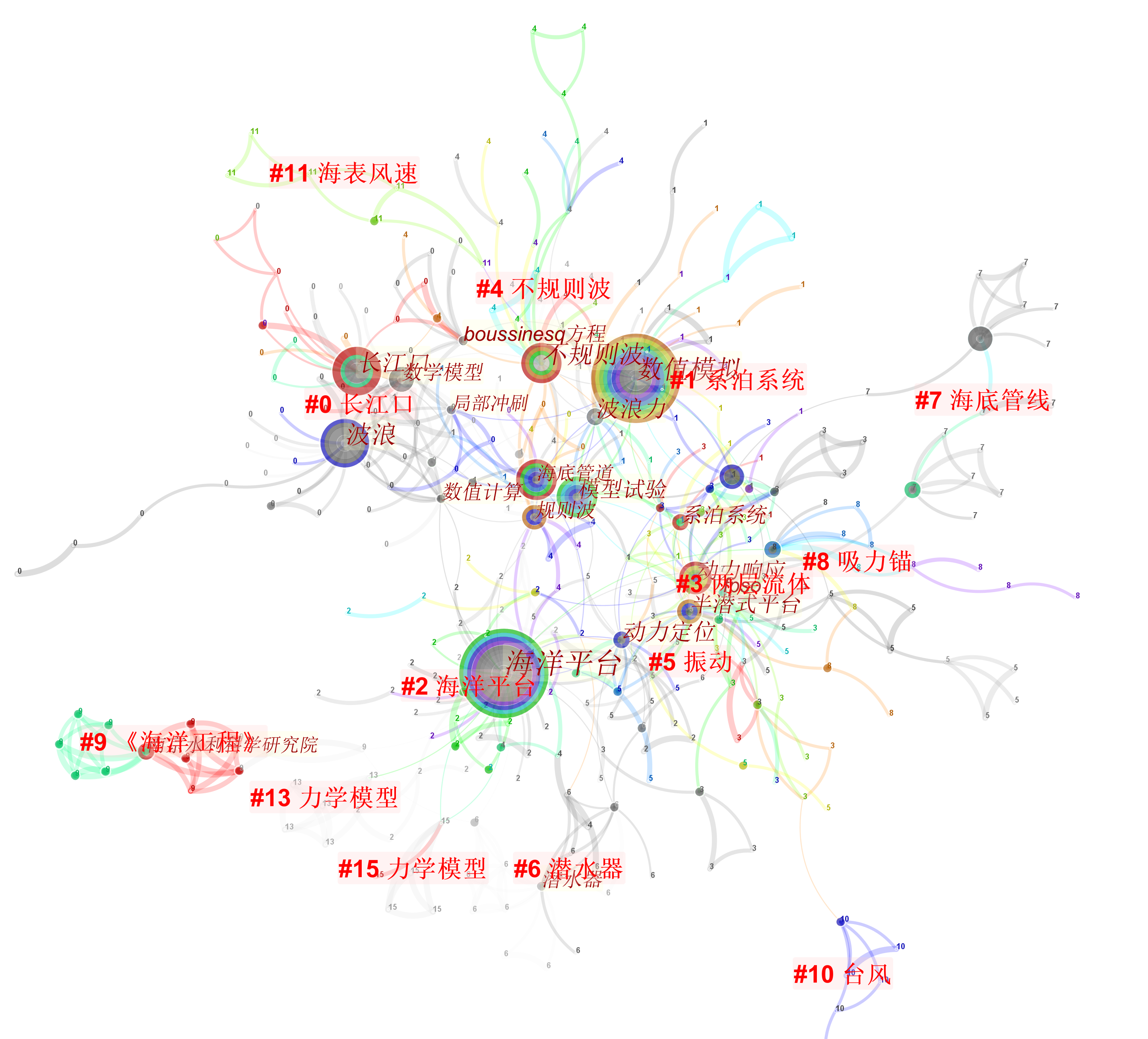
这张图表明《海洋工程》文章的主要关注点是系泊系统、海洋平台、力学模拟、吸力锚、不规则波、振动、海表风速、动力响应、海底管线等,此外长江口是唯一一个以海域聚类的文献簇,且强度第一。可见,《海洋工程》发文围绕海洋平台、海底管线、海洋装备等,形成了各类海洋平台装备、水动力影响因子的文献聚类簇,这说明实际上,海洋工程主要是海洋平台(含水面、水下、水中)的工程,主要研究力学、海洋波动影响等。
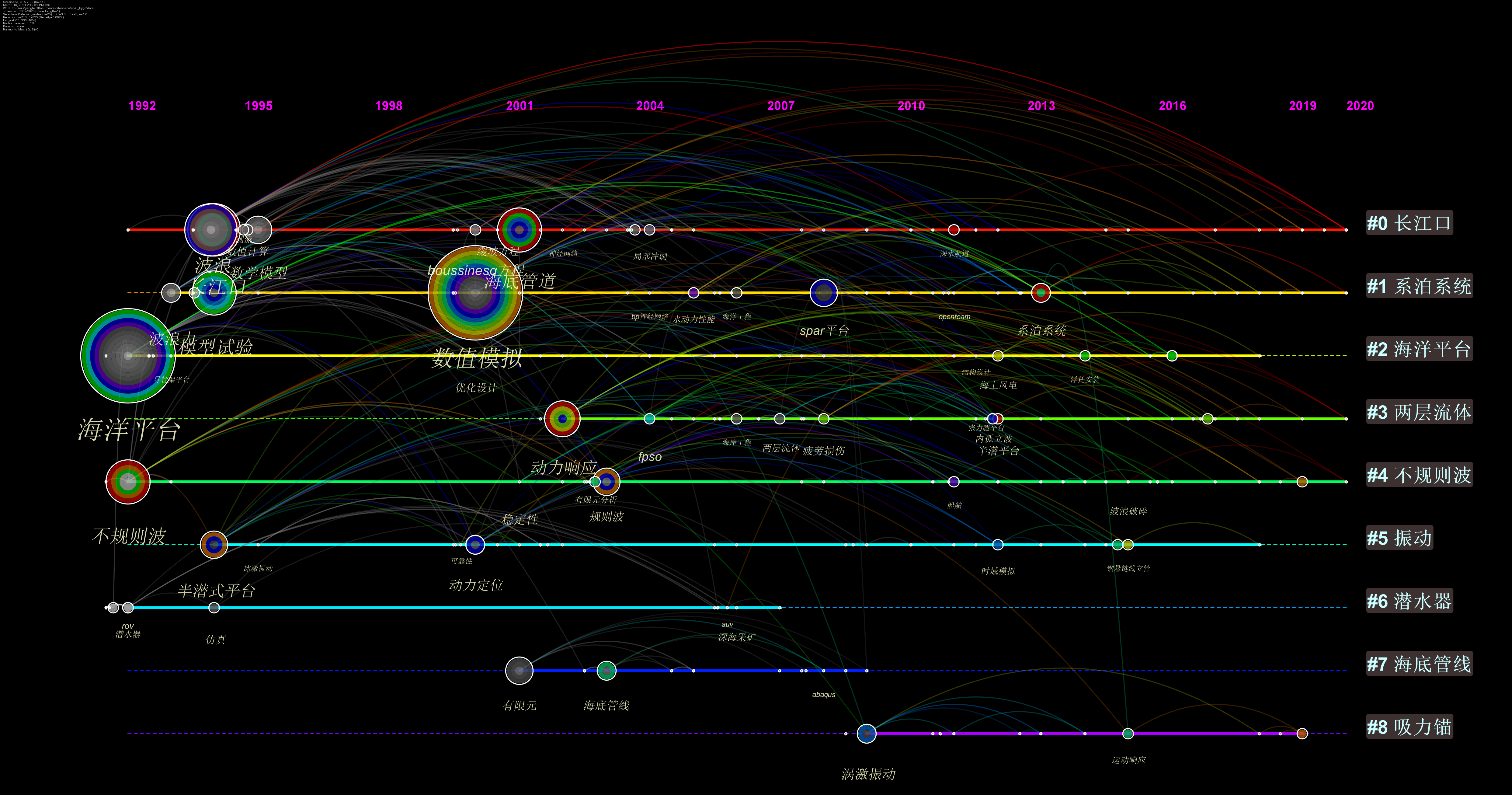
这张时间图谱中不同聚类由平行轴线代表,不同关键词频次由节点大小代表,关键词首次出现年份由位置代,水平线的虚实表示其持续性,#前面的数字表示聚类的强度,0表示最强的聚类簇。从中可以基本判断,长江口持久性最强,说明热度持续,节点连线最为丰富,表明知识流动性好。系泊系统、海洋平台、潜水器、海底管线、吸力锚等平台设施、装备也形成了较强的聚类簇。系泊系统聚类簇自1994年出现,在2000年出现数值模拟的研究热潮。

突现(Burst)是指特定时间段内通过关键词频次的变化将频次高的词探测出来,在一定程度上反映《海洋工程》的研究趋势。与上一幅时间轴的展示相差不多,但此处更加清晰的展现了海洋技术整体的发展趋势,内孤立波、动力响应、系泊系统等关键词为近十年来的主要研究趋势,可见海洋工程从传统的表面风浪因子向内部波动发展。
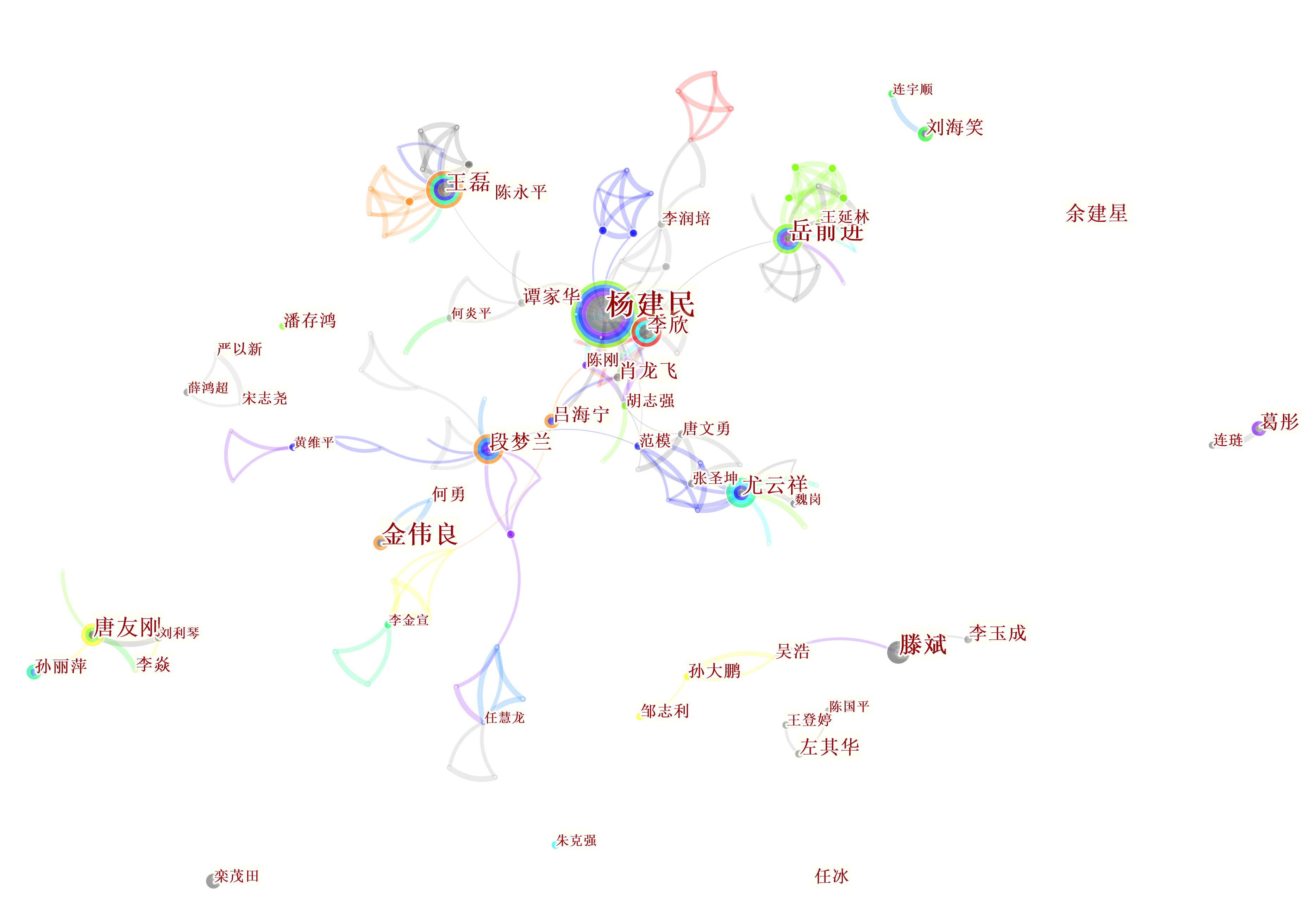
《海洋工程》刊发丰富的海洋技术类文章,不同海洋技术形成了不同的研究人才队伍,因此作者聚类效果明显。颜色的含义为,彩色表示时代较近,灰色表示时代较久。节点大小和位置表示作者的发文频次和中心性。连接线粗细表示不同作者之间的合作强度。
网络中节点的
中心性测量的是网络中节点的位置重要性。有两类节点可能具有较高的中介中心性:1)与其他节点高度相连的枢纽节点;2)位于不同聚类之间的节点。
遗憾的是,CNKI导出的数据不含有引用信息,因此无法通过程序进行文献共引的计量分析,而文献的引用关系最能代表知识的流动脉络。这里,仅列举利用CNKI数据库检索到引用次数最多的前10个文献:
[1]赵志高,杨建民,王磊,程俊勇.动力定位系统发展状况及研究方法[J].海洋工程,2002(01):91-97.
[2]黄维平,刘建军,赵战华.海上风电基础结构研究现状及发展趋势[J].海洋工程,2009,27(02):130-134.
[3]欧进萍,肖仪清,黄虎杰,段忠东,张涛,李维星.海洋平台结构实时安全监测系统[J].海洋工程,2001(02):1-6.
[4]刘学敏,徐玉如.水下机器人运动的S面控制方法[J].海洋工程,2001(03):81-84.
[5]朱克强,李道根,李维扬.海洋缆体系统的统一凝集参数时域分析法[J].海洋工程,2002(02):100-104.
[6]苏玉民,黄胜,庞永杰,徐玉如,吴强.仿鱼尾潜器推进系统的水动力分析[J].海洋工程,2002(02):54-59.
[7]李孟国.海岸河口泥沙数学模型研究进展[J].海洋工程,2006(01):139-154.
[8]李孟国,王正林,蒋德才.近岸波浪传播变形数学模型的研究与进展[J].海洋工程,2002(04):43-57.
[9]李典庆,唐文勇,张圣坤.海洋工程风险接受准则研究进展[J].海洋工程,2003(02):96-102.
[10]余龙,谭家华.基于准静定方法的多成分锚泊线优化[J].海洋工程,2005(01):69-73.
截止本文发布,《海洋工程》被引用最多的文献为赵志高等发表于2002年的动力定位系统发展状况及研究方法,次数为239次,其次为黄维平等人2009年发表的海上风电基础结构研究现状及发展趋势,被引199次。
此外CNKI可以统计文献下载次数,下载频次可反映文献受关注的程度。前五位为:
[1]赵志高,杨建民,王磊,程俊勇.动力定位系统发展状况及研究方法[J].海洋工程,2002(01):91-97.
[2]黄维平,刘建军,赵战华.海上风电基础结构研究现状及发展趋势[J].海洋工程,2009,27(02):130-134.
[3]李孟国.海岸河口泥沙数学模型研究进展[J].海洋工程,2006(01):139-154.
[4]唐友刚,张素侠,张若瑜,刘海笑.深海系泊系统动力特性研究进展[J].海洋工程,2008(01):120-126.
[5]王天英.浅海新型FPSO-IQFP多点系泊系统设计研究[J].海洋工程,2014,32(03):89-95.
通过对核心期刊《海洋工程》1992~2020年的文献计量分析,从期刊引文、关键词突现和研究热点时序聚类分析发现:《海洋工程》所刊论文的主要研究方向为海洋平台以及影响平台稳定性、安全性的相关海洋动力学分析,不同的动力因子以及不同平台类型分别形成各自的文献集合,并且研究热点正在从表面波浪向内孤立波转变,潜水器也以成为当下的一个聚类簇;5家国家实验室是该领域的龙头,然而机构合作指数偏低。
科学、技术、工程关联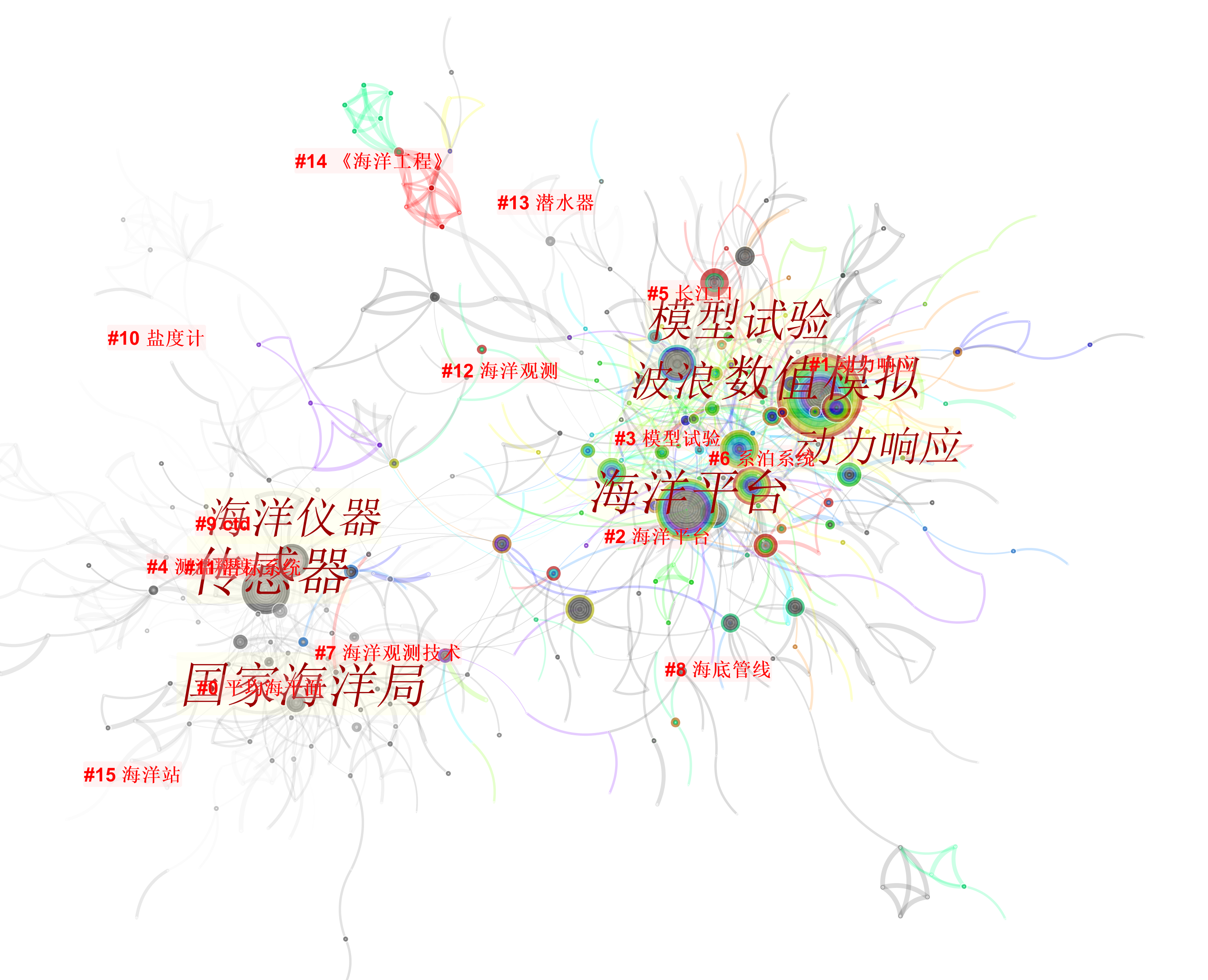
我们把技术和工程的文献打包分析,得到上面的关键词图谱,海洋观测的聚类稍微在二者之间建立联系,但相对较弱。
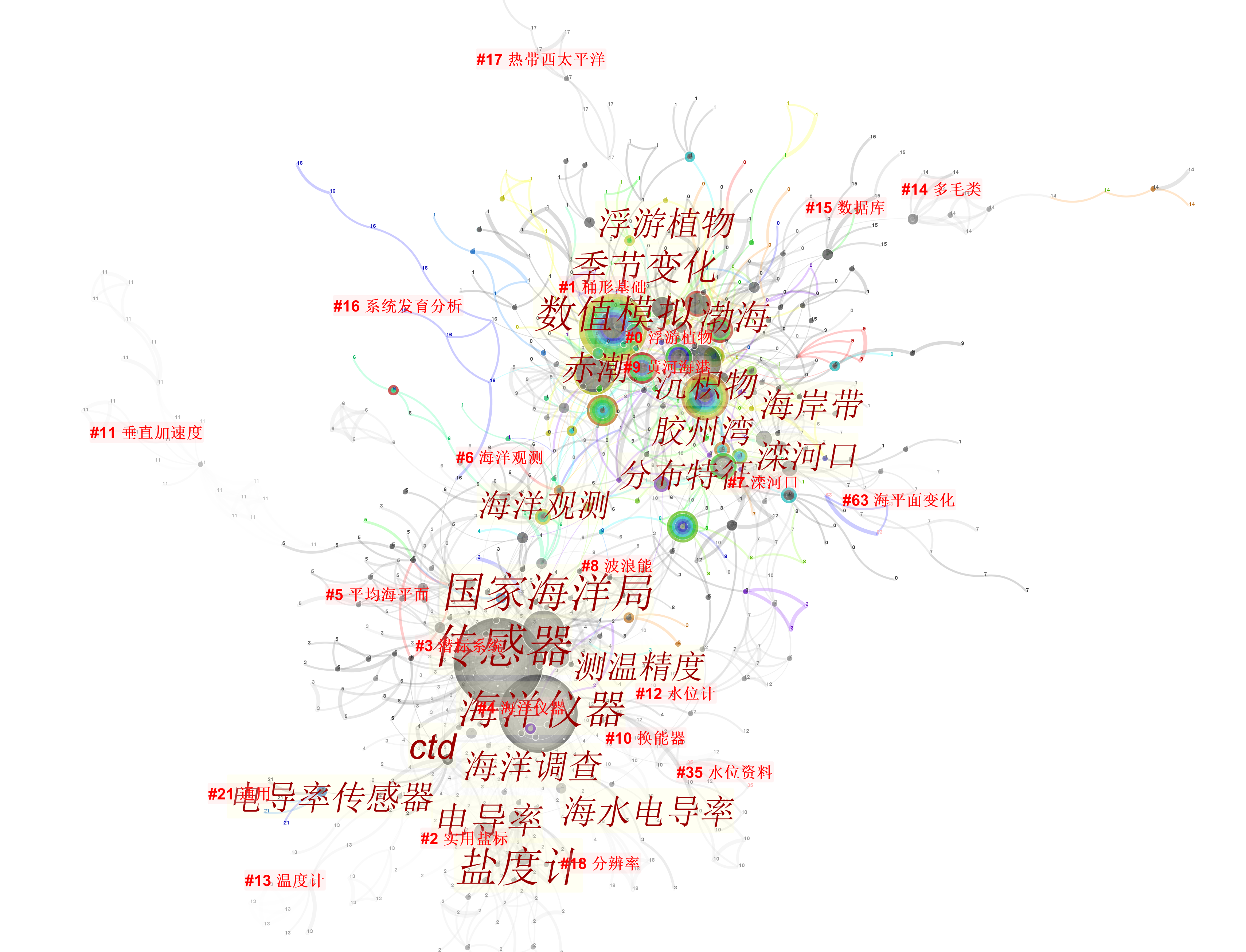
我们把技术和科学的文献打包分析,得到上面的关键词图谱,海洋观测的聚类在二者之间建立较强联系。
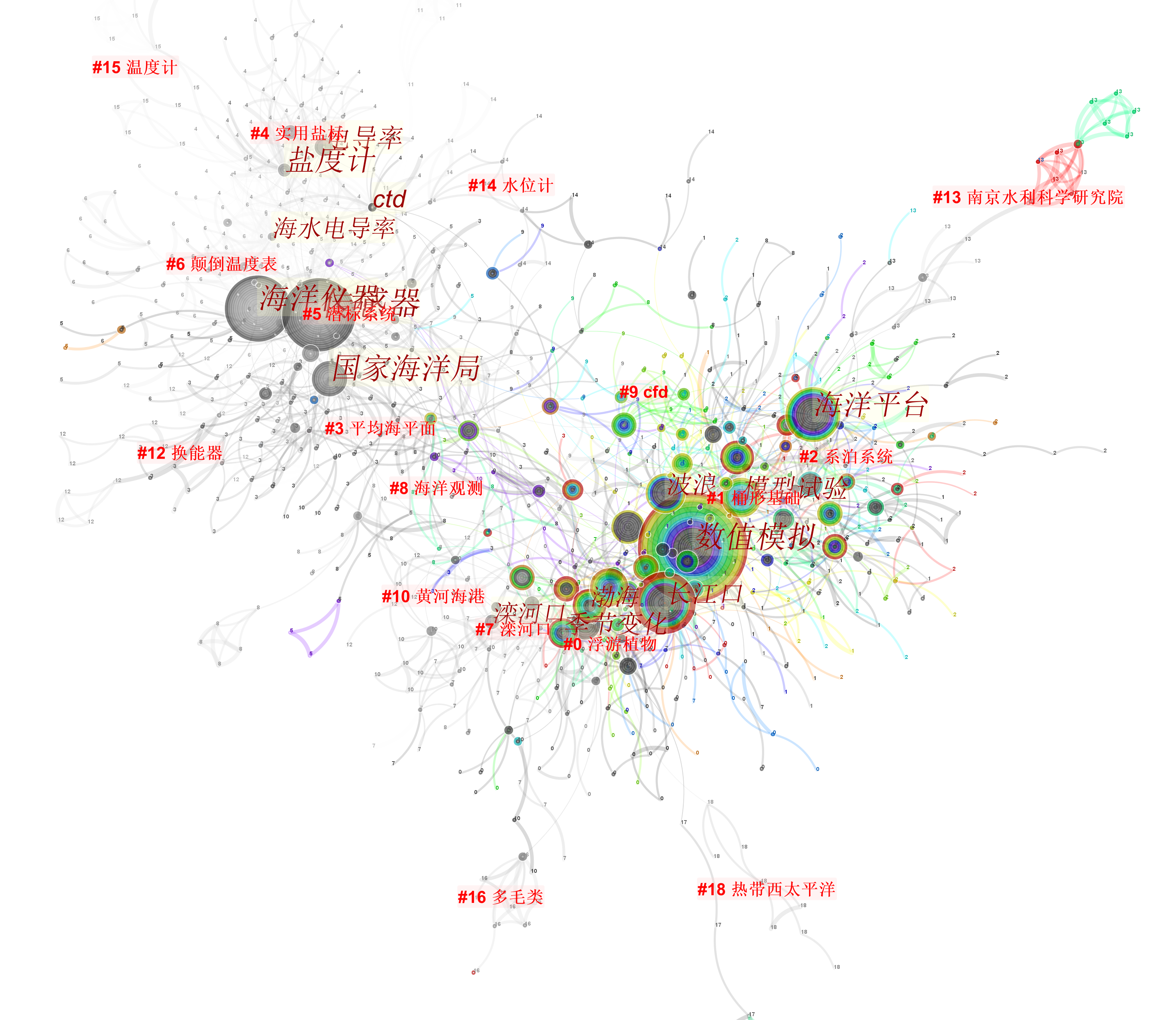
我们把科学、技术和工程的文献打包分析,得到上面的关键词图谱,数值模拟、长江口的聚类在科学和工程之间建立强烈联系。
因其中隐含的信息量太大,作者未来将撰写一份详细的中国海洋科学技术以及工程应用的情报分析文章。
上一篇的研究对象是《海洋科学进展》,本文研究海洋领域另一份北大核心期刊《海洋技术学报》。首先
科学和技术的区别和联系将在大数据分析下清晰呈现,其次我国海洋技术过去45年的发展经历也可通过文献计量学展示。
以中国知网1976~2020年间的北大核心期刊《海洋科技术学报》文献记录为研究对象,运用文献计量分析方法可视化分析《海洋技术学报》所发表论文的研究内容及其演变。研究表明,《海洋技术学报》期刊的研究内容主要涉及海洋仪器、清洁海洋能、海洋观测技术等方面。研究论文主要以设备类型组成文献簇,所涉及海洋设备主要包含浮标站、实用盐标、电导率传感器、剖面浮标、水位计、垂直加速度、换能器、深海机器人等,清洁海洋能源方面形成了潮流能、波浪能、海洋能等为主题的聚类簇,发文趋势分析表明海洋技术的关注点正从传统的要素观测技术逐渐向清洁能源技术转变。研究机构以国家海洋技术中心为主,机构间合作强度偏弱。
文献计量学是利用数学和统计学方法定量分析科技文献外部表征,进而揭示学术研究活动特征,已广泛地应用于多学科领域的发展现状和规律探索。文献计量学可以用于期刊评价,例如核心期刊的遴选,也可以从宏观角度揭示某一种学科的发展规律,并在微观角度揭示学科的知识流动。
本文将使用文献计量方式分析《海洋技术学报》历年发文情况,制作关键词、作者、机构等知识共现谱图,通过共现聚类使主要研究内容、人员、机构的分布和关联清晰展现。因为受知识水平限制,本文不做过多的微观解释分析,主要以知识图谱展示,从宏观角度展现《海洋技术学报》。
《海洋技术学报》(中文·双月刊,刊号:CN12-1435/P),原名《海洋技术》,创刊于1982年,是我国唯一以刊载海洋技术研究成果为主要内容的专业期刊,自2000年起入选全国中文核心期刊,并被联合国《水科学和渔业文摘(ASFA)》收录。多年来,《海洋技术学报》为我国海洋技术研究和应用积累了大量科技文献,为国家海洋主管部门提供了重要的决策依据,为我国海洋工程仪器装备研发起到了积极的促进作用。
由于《海洋技术学报》曾用名《海洋技术》,因此中国知网检索:
JN=海洋技术学报 OR JN=海洋技术
此处,一般应剔除卷首语、编辑部声明等文献,进而得到纯粹的科学研究文献。
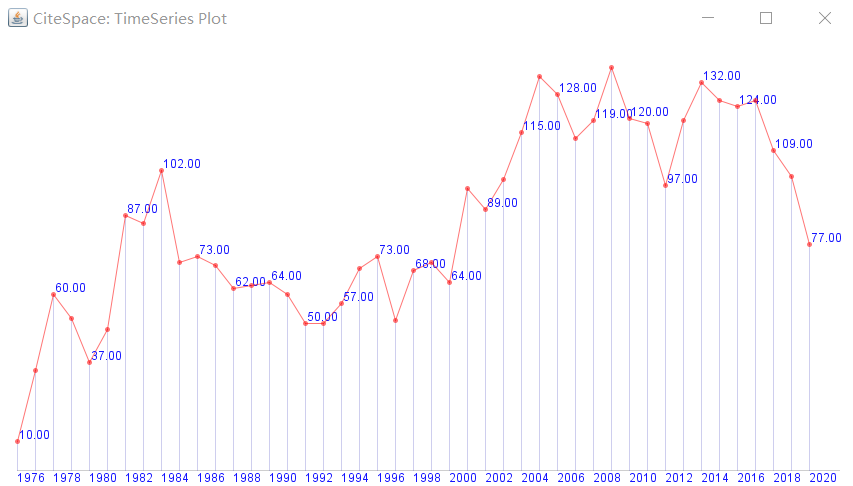
1976-2020年共发表3796篇文章,年发文不超过140篇,发文量在同类期刊属于中游水平。
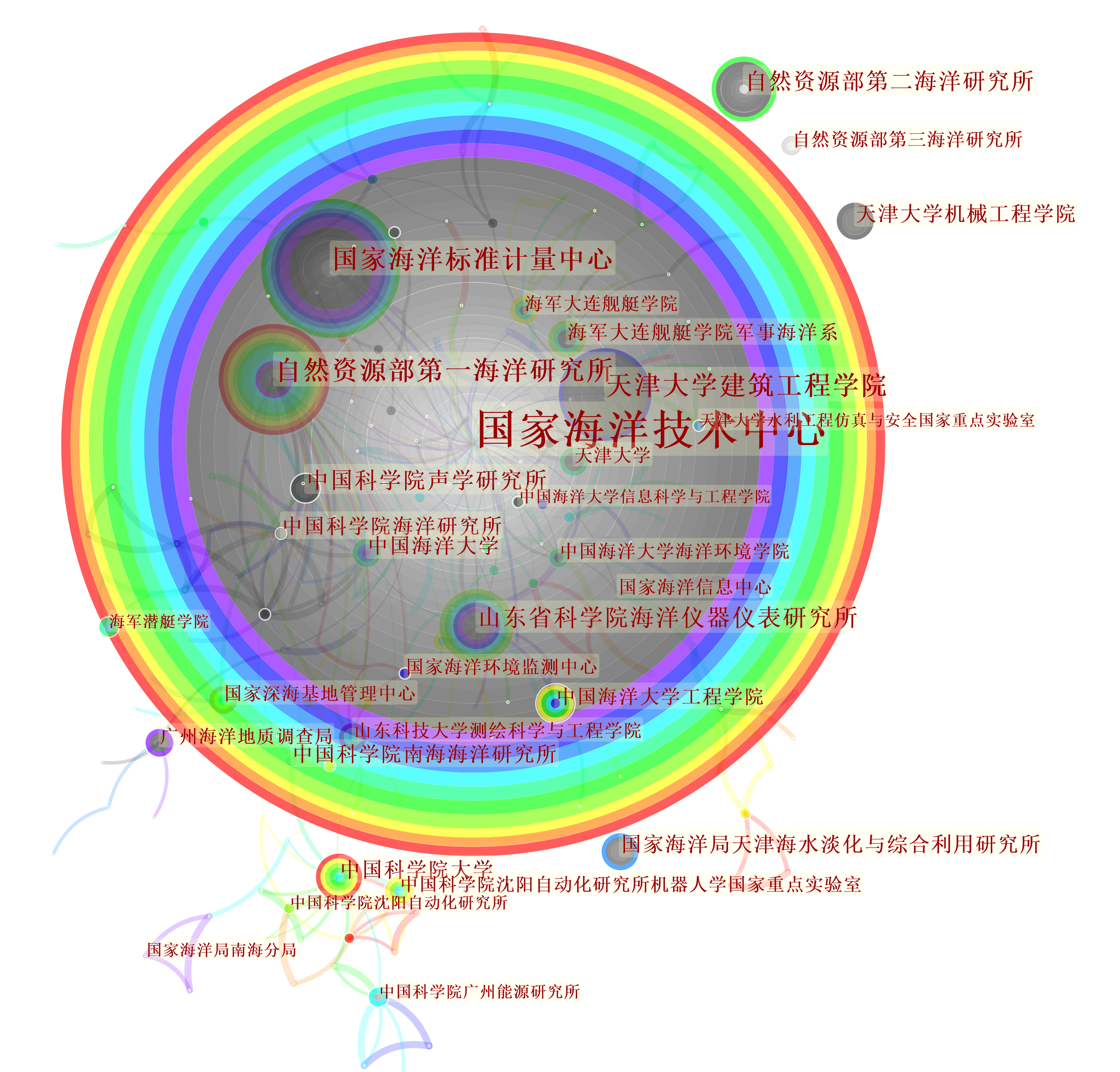
机构节点数共计1051个(表示研究单位总数),共现连接线415(表示合作关系),各单位之间合作关系相对上一篇《海洋科学进展》所得结论(比例接近1:1)偏弱。
发文最多的单位为国家海洋技术中心,表现在图谱上的特点就是节点中心性强,节点圈大(最大的圈),其文献的节点数超过831。其次为国家海洋标准计量中心和自然资源部第一海洋研究所,其文献的节点数均为69,第一和第二之间的发文数量差距较大。
图中的节点(圆圈)的颜色表示时间,灰色表示年代久远的文献,彩虹色表示为近几年的文献。比如国家海洋技术中心内部为灰色,外部为彩虹色,表示其文献的历史较早,且至今活跃在海洋技术一线,而自然资源部第一海洋研究所主要为彩色,表示近几年才开始较多的发表海洋技术方向文章。
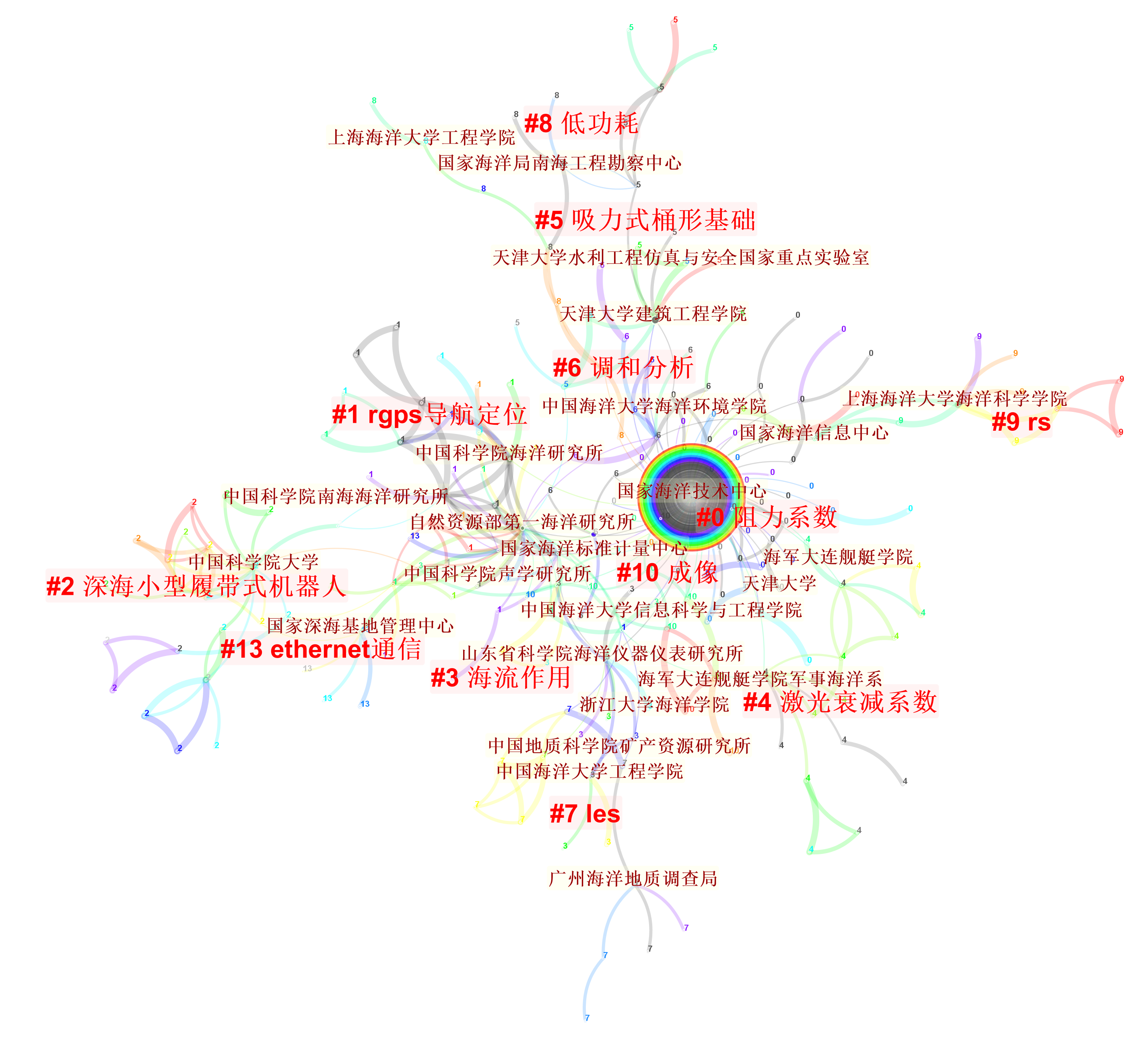
这张图展示的是研究机构和关键词的共现聚类,通俗理解为研究机构的研究兴趣。
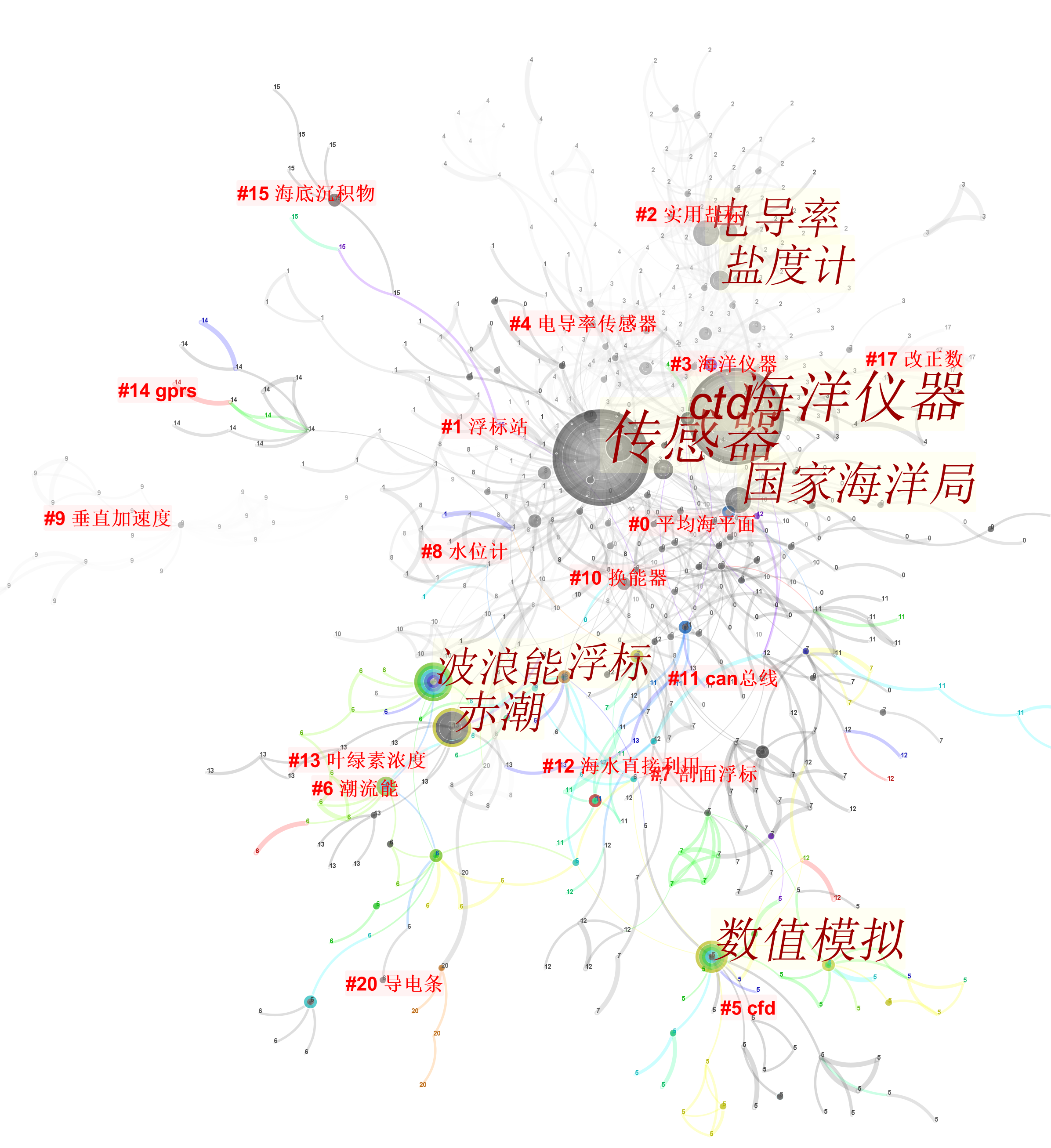
这张图表明《海洋技术学报》文章的主要关注点是平均海平面、浮标站、实用盐标、海洋仪器、电导率传感器、CFD流体动力学分析、潮流能、剖面浮标、水位计、垂直加速度、换能器等。可见,《海洋技术学报》发文围绕海洋传感器,形成了各类海洋传感器或者传感器主要参数的文献聚类簇,这说明实际上,海洋技术主要是海洋测量装备的技术。

这张时间图谱中不同聚类由平行轴线代表,不同关键词频次由节点大小代表,关键词首次出现年份由位置代,水平线的虚实表示其持续性,#前面的数字表示聚类的强度,0表示最强的聚类簇。从中可以基本判断,平均海平面持久性最强,说明热度持续,节点连线最为丰富,表明知识流动性好。浮标站、盐标、剖面浮标等具体的设备也形成了较强的聚类簇,然而有些设备研究的热度已过。潮流能自1986年首次出现在《海洋技术学报》,愈发活跃。CFD流体动力学分析聚类簇自1998年出现,也活跃至今。
然而,疑问来了,这里的平均海平面是海平面变化研究吗?答案是否。形成平均海平面的关键词为:
平均海平面; 操作经验; 卫星轨道; 声学水位计; 海平面变化; 海流剖面; 产品标准; 大地水准面; 卫星测高技术; 水尺零点 | 压力式验潮仪; 海平面资料; 标准偏差; 澳大利亚; 操作经验; 海流剖面; 回波信号; bradly; 美国国家海洋大气局; 卫星轨道; 平均海平面 (33.1, 1.0E-4); 验潮仪 (16.44, 1.0E-4); 海平面变化 (12.31, 0.001); 水位测量系统 (12.31, 0.001); 基准面 (12.31, 0.001); 压力式验潮仪 (12.31, 0.001); 海平面高度 (12.31, 0.001); 国家海洋局 (9.34, 0.005); 澳大利亚 (8.19, 0.005); 海平面测量 (8.19, 0.005); 现状 (8.19, 0.005); 海平面资料 (8.19, 0.005); 验潮井 (8.19, 0.005); 海平面 (8.19, 0.005); “九五”期间 (8.19, 0.005); 海洋领域 (8.19, 0.005); 高新技术 (8.19, 0.005); 压力验潮仪 (8.19, 0.005); 办事处 (8.19, 0.005); 校准管 (8.19, 0.005); 标准偏差 (4.65, 0.05); 数据处理 (4.65, 0.05); 产业化 (4.09, 0.05); 潮汐分析 (4.09, 0.05); 兰佩杜萨 (4.09, 0.05); kuo (4.09, 0.05); 科技情报所 (4.09, 0.05); 传播时间 (4.09, 0.05); 压力式水位计 (4.09, 0.05); 声学水位计 (4.09, 0.05); 管理 (4.09, 0.05); 海流剖面 (4.09, 0.05); 海洋监测技术 (4.09, 0.05); psmsl (4.09, 0.05); 深海锰结核 (4.09, 0.05); 仪器技术 (4.09, 0.05); 快速充电 (4.09, 0.05); 研究 (4.09, 0.05); bradly (4.09, 0.05); 操作经验 (4.09, 0.05); 丰度分布 (4.09, 0.05); 海图基准面 (4.09, 0.05); 测地学 (4.09, 0.05); hyb (4.09, 0.05); 科技情报网 (4.09, 0.05); 卫星测高技术 (4.09, 0.05); 精确测定 (4.09, 0.05); 制备 (4.09, 0.05); 溶液 (4.09, 0.05); 同步观测 (4.09, 0.05); 标准化 (4.09, 0.05); 斜压模式 (4.09, 0.05); 倒置式 (4.09, 0.05); 浮子式水位计 (4.09, 0.05); 多普勒跟踪系统 (4.09, 0.05); 动力高度 (4.09, 0.05); 回波信号 (4.09, 0.05); 产品标准 (4.09, 0.05); 不间断电源 (4.09, 0.05); 国内 (4.09, 0.05); 声学技术 (4.09, 0.05); 《论十大关系》 (4.09, 0.05); 美国国家海洋大气局 (4.09, 0.05); 变异性 (4.09, 0.05); ctd测量技术 (4.09, 0.05); 哈尔滨市 (4.09, 0.05); 发展 (4.09, 0.05); 探查技术 (4.09, 0.05); 产品展销 (4.09, 0.05); 国务院 (4.09, 0.05); 电离层误差 (4.09, 0.05); 绝缘箱 (4.09, 0.05); 阿巴科 (4.09, 0.05); 水利电力部 (4.09, 0.05); 世界大洋环流实验 (4.09, 0.05); 巴哈马 (4.09, 0.05); 雷达测高仪 (4.09, 0.05); 水尺零点 (4.09, 0.05); 分布特征 (4.09, 0.05); 波浪作用 (4.09, 0.05); 国际先进水平 (4.09, 0.05); 验潮水准点 (4.09, 0.05); 富集区 (4.09, 0.05); 仪器设备 (4.09, 0.05); 卫星轨道 (4.09, 0.05); 大地水准面 (4.09, 0.05); 环境监测 (4.09, 0.05); 激光站 (4.09, 0.05); 电导率 (2.21, 0.5); 实用盐标 (1.93, 0.5); 盐度计 (1.65, 0.5); 卫星高度计 (1.59, 0.5); 信噪比 (1.59, 0.5); 颠倒温度表 (1.37, 0.5); 海水电导率 (1.37, 0.5); 电导率传感器 (1.37, 0.5); 实用盐度 (1.37, 0.5); 浮标站 (1.09, 0.5); 海洋水文气象 (1.09, 0.5); 实验室盐度计 (1.09, 0.5)
可见平均海平面聚类簇依然围绕着测量海水水位的相关设备和技术,而非海平面变化分析、气候变化研究等科学主题。因为期刊创刊与1976年,恰文革末年,论十大关系、四人帮等关键词也出现在了这个聚类簇。
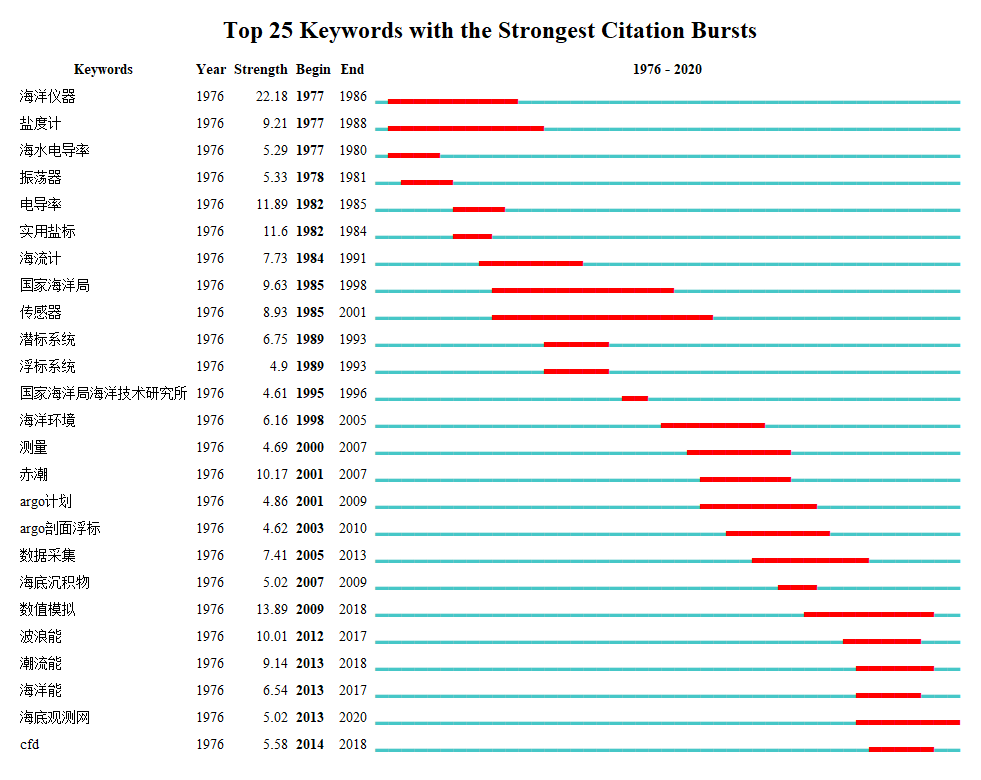
突现(Burst)是指特定时间段内通过关键词频次的变化将频次高的词探测出来,在一定程度上反映《海洋技术学报》的研究趋势。与上一幅时间轴的展示相差不多,但此处更加清晰的展现了海洋技术整体的发展趋势,数值模拟、CFD、潮流能、波浪能、海洋能等关键词为近十年来的主要研究趋势,可见海洋技术从传统的要素观测逐渐向清洁能源技术演变。
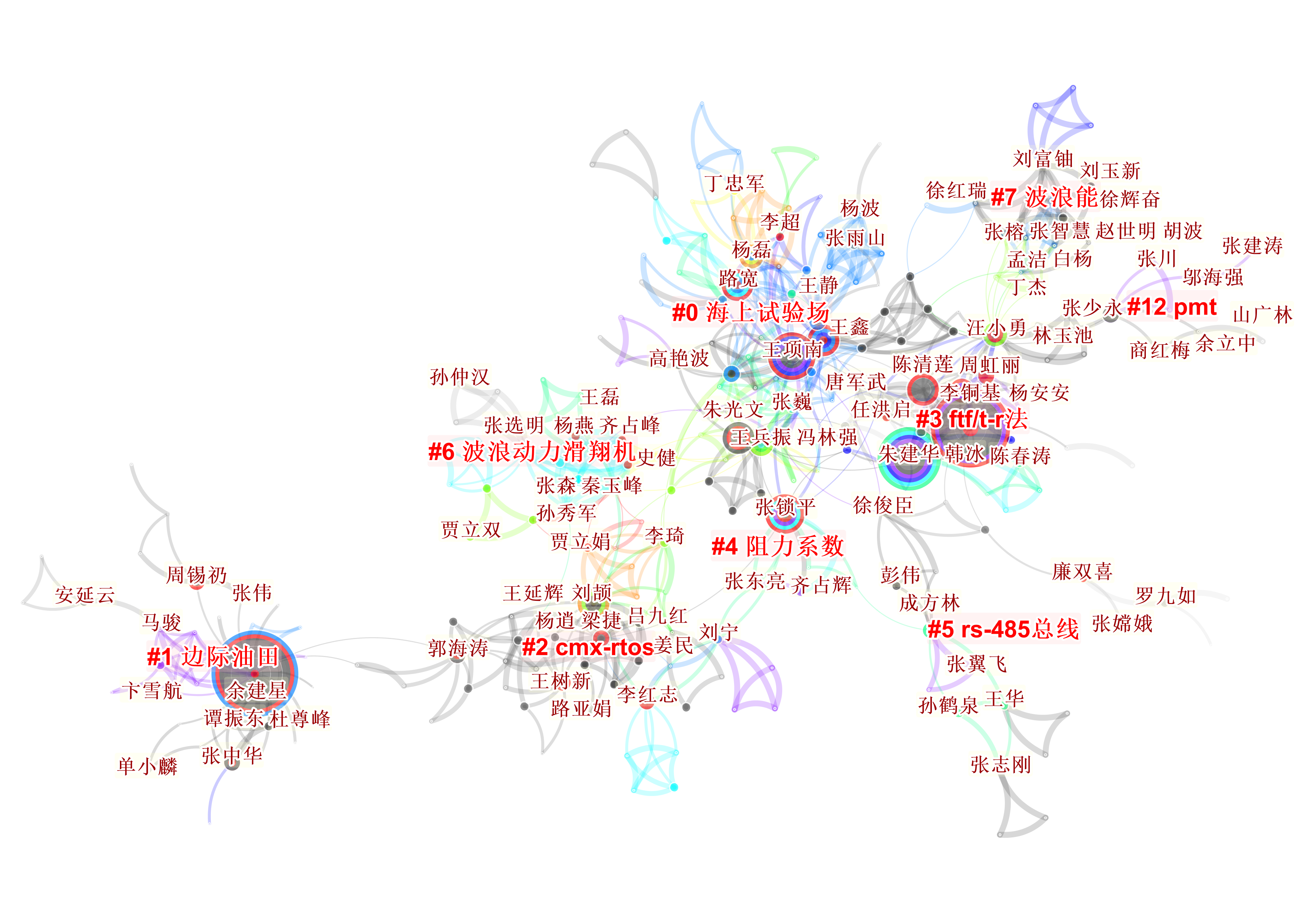
《海洋技术学报》刊发丰富的海洋技术类文章,不同海洋技术形成了不同的研究人才队伍,因此作者聚类效果明显。颜色的含义为,彩色表示时代较近,灰色表示时代较久。节点大小和位置表示作者的发文频次和中心性。连接线粗细表示不同作者之间的合作强度。
网络中节点的
中心性测量的是网络中节点的位置重要性。有两类节点可能具有较高的中介中心性:1)与其他节点高度相连的枢纽节点;2)位于不同聚类之间的节点。
遗憾的是,CNKI导出的数据不含有引用信息,因此无法通过程序进行文献共引的计量分析,而文献的引用关系最能代表知识的流动脉络。这里,仅列举利用CNKI数据库检索到引用次数最多的前5个文献:
[1]李守军,包更生,吴水根.水声定位技术的发展现状与展望[J].海洋技术,2005(01):130-135.
[2]尹建华,吕庆春,阮国岭.低温多效蒸馏海水淡化技术[J].海洋技术,2002(04):22-26.
[3]朱光文.我国海洋监测技术研究和开发的现状和未来发展[J].海洋技术,2002(02):27-32.
[4]高艳波,李慧青,柴玉萍,麻常雷.深海高技术发展现状及趋势[J].海洋技术,2010,29(03):119-124.
[5]成方林,张翼飞,刘佳佳.基于“北斗”卫星导航系统的长报文通信协议[J].海洋技术,2008(01):26-28+31.
截止本文发布,《海洋技术学报》被引用最多的文献为李守军等发表于2005年的水声定位技术的发展现状与展望,次数为231次,其次为尹建华等人2002年发表的低温多效蒸馏海水淡化技术,被引128次。
此外CNKI可以统计文献下载次数,下载频次可反映文献受关注的程度。前五位为:
[1]高从堦,周勇,刘立芬.反渗透海水淡化技术现状和展望[J].海洋技术学报,2016,35(01):1-14.
[2]尹建华,吕庆春,阮国岭.低温多效蒸馏海水淡化技术[J].海洋技术,2002(04):22-26.
[3]刘海笑,黄泽伟.新型深海系泊系统及数值分析技术[J].海洋技术,2007(02):6-10.
[4]刘莉娜,陈里娥,韦萍萍,李喻春,廖文波,昝启杰.深圳福田红树林自然保护区的生态问题及修复对策研究[J].海洋技术,2013,32(02):125-132.
[5]高艳波,李慧青,柴玉萍,麻常雷.深海高技术发展现状及趋势[J].海洋技术,2010,29(03):119-124.
通过对核心期刊《海洋技术学报》1967~2020年的文献计量分析,从期刊引文、关键词突现和研究热点时序聚类分析发现:《海洋技术学报》所刊论文的主要研究方向为海洋仪器设备以及清洁海洋能源,不同的海洋技术装备以及不同类型的新型海洋能分别形成各自的文献集合,并且研究热点正在从传统观测技术向海洋新能源采集技术转变,和国家的能源发展战略一致(如清洁能源)。
从《海洋科学进展》和《海洋技术学报》的文献计量比较,可知科学主要围绕经典的海洋学科(如,物理海洋、海洋地质、生物化学等),进行数据分析和理论研究等,技术主要涉及海洋观测仪器装备、新能源装备技术等,主要研究数据的观测技术等。二者另一个重要的区别是机构间合作强度不同,科学比技术高了一倍,可能的原因是技术类研究更加注重知识产权保护,分享和合作动力偏低,科学研究则更加重视机构合作,通过合作来获得更好的共赢效果,科学家的分享和合作动力较高。