0%

SWOT观测亚中尺度过程

发表于 更新于 阅读次数： Valine：

海洋运动的时空尺度

Temporal and spatial scales for a variety of ocean processes (adapted from Dickey and Bidigare [2005]

海洋中存在着各种时间空间尺度的运动，从全球洋流尺度到中尺度涡旋，到重力波，直至小尺度的湍流混合过程。海洋的运动无时无刻不在塑造着地球的气候和生态系统。然而，有一类既不大也不小的动力现象，它们介于中尺度涡流和小尺度湍流之间，这就是亚中尺度洋流（Submesoscale Currents，简称SMCs）。这些涡旋在海洋中很常见，它们可以影响海洋中营养物质的分布，进而影响海洋生态系统。

亚中尺度小科普

亚中尺度运动是指那些水平长度在数十米到10公里，垂直高度在数十到数百米，演化时间尺度为数小时到数天的洋流现象。
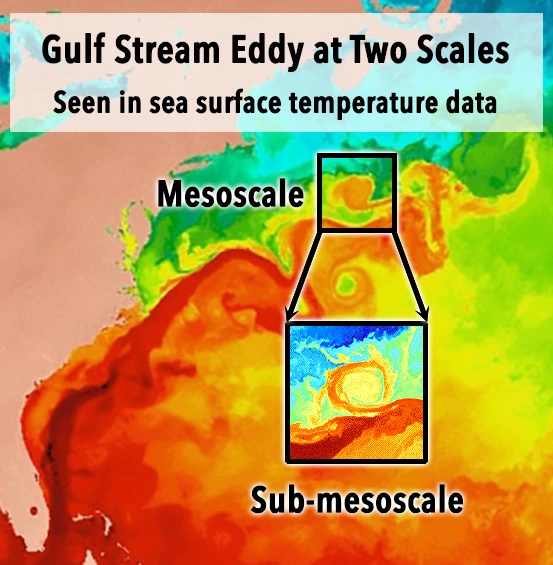
在海洋表面，我们可以通过仔细观察发现一些特殊的线条，这些线条实际上是由水流和海洋生物分布的不均匀性形成的。这些线条很难在单一的剖面图或者时间序列图中辨认出来，因为它们可能和其他类型的水流混合在一起。但是，如果我们能够从高空或者使用卫星图像来观察，就能够看到这些线条的全貌。

这些线条是海洋中亚中尺度海流的明显标志。它们可能表现为海面上温度或盐度的突然变化，或者海洋生物如浮游植物的密集分布。这些线条的形成，与海洋中的锋面和丝状物有关。

锋面就像是海洋中的一道墙，一侧是温暖的水，另一侧是冷水；而丝状物则是这些锋面中的细线，它们可以是温暖的水流，也可以是冷水。通过高分辨率的卫星图像，我们可以清晰地看到这些线条的分布。比如在地中海，由于海面上的浮渣（一种由生物产生的物质）聚集，形成了螺旋状的线条，这些线条实际上是由海洋中的亚中尺度涡旋造成的。这些涡旋可以很大，直径约5公里，线条宽度约100米。

研究发现，这些流线常常与海洋中的锋面有关。锋面是海洋中密度梯度很大的区域，它们可以是由风或者水流的剪切力形成的。在锋面附近，水流可能会变得更加混乱和复杂，形成许多小的涡旋。SMCs通常超出了准地转理论（通常用于中尺度涡旋的理论框架）的范畴，但仍然受到地球自转和海洋稳定的密度分层的强烈影响。

Gulf Stream eddy at two scales.

由于其独特的空间和时间尺度，亚中尺度洋流的研究长期以来受到技术限制。传统的船只、浮标和卫星观测手段难以捕捉到这些现象。然而，近年来随着高分辨率卫星影像、多重嵌套计算模拟方法的发展，以及大量表面漂流器的应用，科学家们开始能够更好地观测和研究亚中尺度洋流。

SWOT探测亚中尺度

亚中尺度的水平尺度范围未有定论，有文献从物理角度认为0.1–10km，也有文献认为是传统高度计无法探测的10-100km可称之为亚中尺度。此处，我们忽略这种矛盾。

由于SMCs复杂的动态特征和对海洋生态系统的显著影响，研究人员一直在寻找更精确的方法来探测和理解这些洋流。SWOT卫星的出现，为这一研究带来了突破性的进展。

SWOT卫星主要科学目标是精确测量全球海洋、湖泊和河流的水位变化。这颗卫星配备了雷达干涉测高仪，可以以前所未有的高分辨率捕捉海洋表面高度的微小变化。这一技术优势使得SWOT成为研究亚中尺度洋流的理想工具。

从SWOT L3产品计算动力参数

海面高度异常SLA是指海平面相对于平均海平面的偏差。SLA数据提供了海洋表面动力的重要信息，通过这些数据，可以推导出海洋表层流速、动能和涡度。从SWOT发布的SLA L3产品计算速度、动能、涡度以及波数谱，是研究亚中尺度动力过程的基本步骤。

  1. 计算速度（Velocity）：
    海面高度异常可以用于计算地转流速。假设我们有一个二维的SLA场 $(\eta(x, y))$，可以通过以下公式计算地转流速分量：
    $$
    u = -\frac{g}{f} \frac{\partial \eta}{\partial y}
    $$
    $$
    v = \frac{g}{f} \frac{\partial \eta}{\partial x}
    $$
    其中，$u$ 和 $v$ 分别是东西向和南北向的流速分量，$g$ 是重力加速度，$f$ 是科里奥利参数，$\eta$ 是海面高度异常。

  1. 计算动能（Kinetic Energy）：
    一旦得到了流速分量$u$ 和$v$，可以计算流体动能。动能（KE）可以通过以下公式计算：
    $$
    KE = \frac{1}{2} (u^2 + v^2)
    $$

  1. 计算涡度（Vorticity）：
    涡度是描述流体旋转性的一个重要参数。对于二维流场，可以通过以下公式计算涡度 $(\zeta)$：
    $$
    \zeta = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}
    $$
    涡度的正值表示逆时针旋转，而负值表示顺时针旋转。

L4产品速度和动能分析

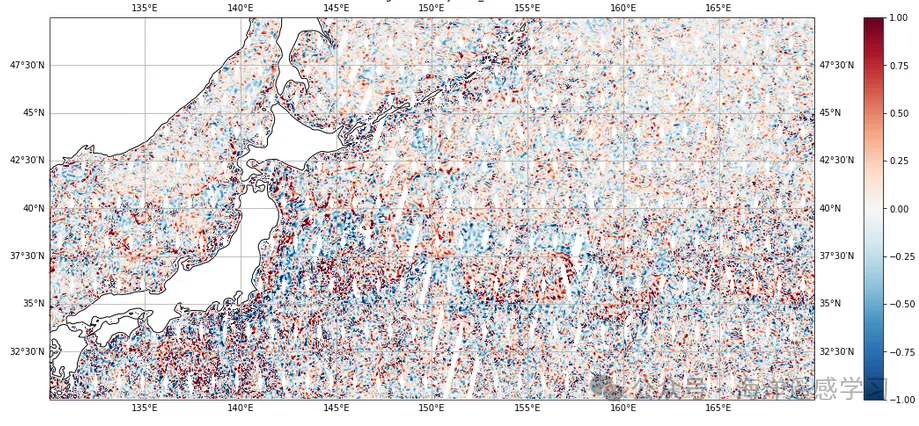
AVISO近期发布了包含速度和涡度参数的SLA L4融合产品。由于覆盖范围的不同，在21天重复轨道期间，各个位置的观测次数随纬度变化显著：赤道附近约为两次，中纬度地区为两到四次，高纬度地区则超过六次。这种时间采样对研究亚中尺度快速海洋过程带来了挑战，特别是那些时间尺度与采样间隔相当或更短的现象。

以下是一些分析计算结果：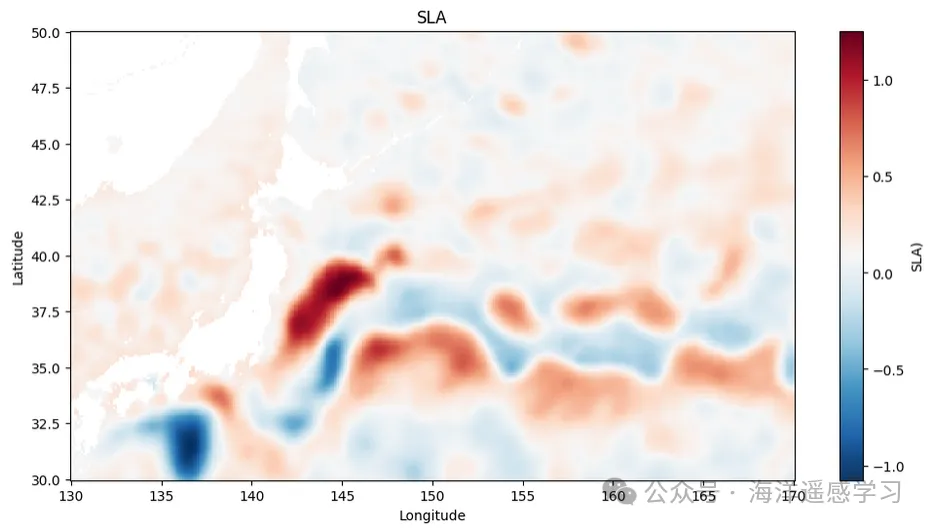



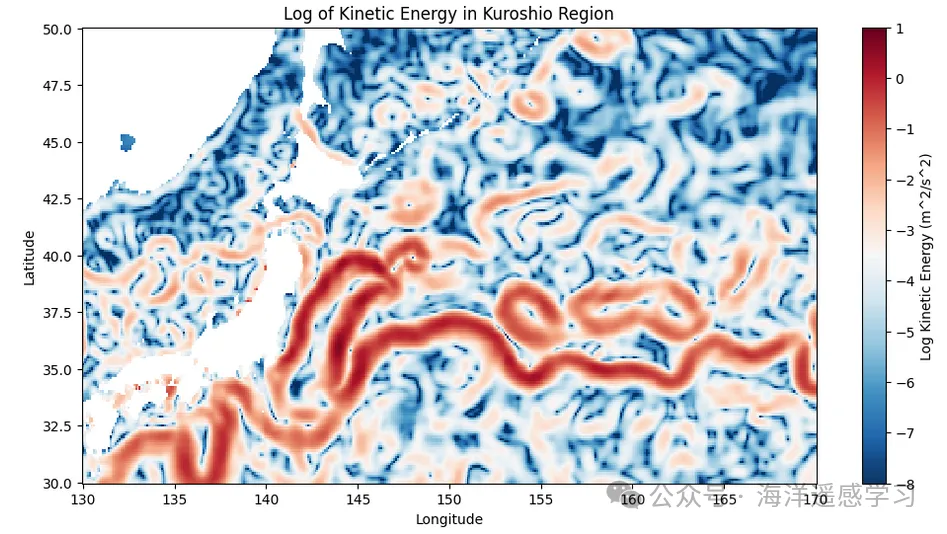
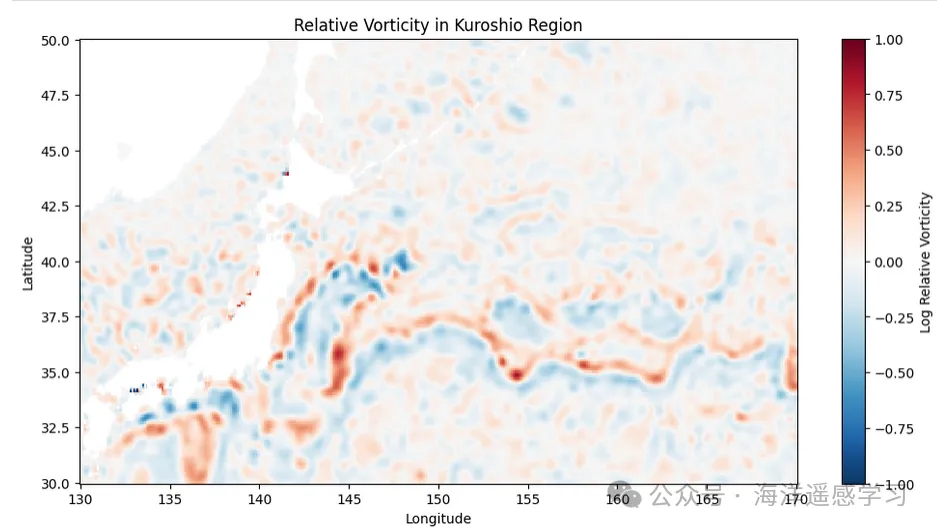
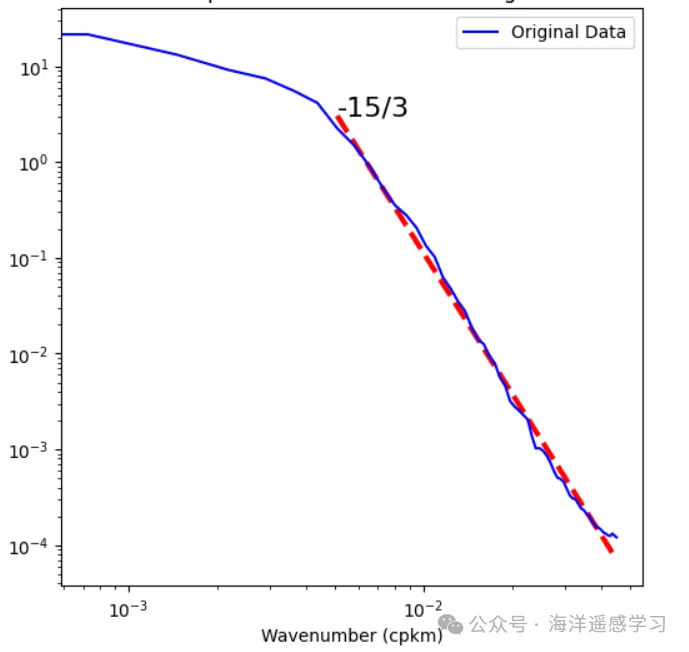
计算KE的波数谱，发现斜率的幂率特别好，可以一直到20km附近。然而，不知道何种原因，其斜率却是-15/3，这和QG、SQG理论的都不一致，并且也没有反应出来内波连续体的隆起。这个问题以后需要花时间研究。

SWOT研究亚中尺度的挑战和机遇

SWOT 的精细尺度海面高度观测提供的主要挑战和机遇是研究这些平衡的海洋运动（由地球自转、风和浮力效应驱动）与内部潮汐和内部重力波的相互作用，这些潮汐和内部重力波在海洋表面下搅动和循环水。虽然大部分内潮是可预测的，但内波连续体却不是。

建模研究表明，SSH中平衡运动与内波明显分离的空间尺度随地理和季节而变化[ Qiu et al. ，2018]。平衡运动在中高纬度地区占主导地位，内波在能量较弱的东部盆地和热带地区尤为突出。与SWOT和原位系统同时对这些过程进行充分观察，应该可以在测试方法上取得进展，以分离这两种纠缠的运动并了解它们的相互作用。

旋转分层湍流的理想化模拟表明，在某些地方（如强流和涡流中），SMCs应该是活跃的。目前还没有现实的海洋模拟或测量明确显示这一点，但也没有对此问题进行过深入研究。
如果这一假设成立，可以预期会有相对浅的动能谱、正向能量级联以及提高的耗散和越密度混合率。