0%

卫星高度计的物理海洋应用系列 - 西边界流

发表于 更新于 阅读次数： Valine：

最近公布的2023年院士评选结果出炉了，我并未入选。但坦白说，这对我，乃至我的粉丝们来说，实际上是一件好事。若我真成了院士，必将被繁杂的事务和没完没了的会议所困。如此一来，我又如何能有足够的时间和精力，去投入到我所热爱的科研和科普工作中呢？

其实，成为院士，并不能改变一个人的本质。戴上这顶帽子，不代表你就更优秀。作为一名科研工作者，我们追求的是在科学的长河中留下独特的印记，为这个社会贡献自己的力量。从这个初心出发，我们应当始终追求更高的目标。

不得不说，这件事也影响了我为粉丝们写作的计划。我的粉丝数量增长放缓，偶尔还会掉粉，这让我颇感心痛。为此，我制定了一项新的写作计划，专注于撰写一系列关于卫星高度计在物理海洋学方面应用的文章。在这个系列中，我将深入探讨卫星高度计技术如何帮助我们更好地理解海洋，特别是在中尺度和行星尺度上的海洋波动研究上。在即将推出的系列文章中，我们将探索多个关键的物理海洋学概念和现象，这个内容丰富且深入的系列将涵盖理论解析与Python编程实践。其主要目的是为海洋遥感领域的研究生群体提供清晰、系统的理论阐述，以及相应的技术实现。完成这一系列内容可能需要数月时间，但我们致力于提供深度且实用的学习资源，以促进对海洋科学的深入理解和研究。

今天我们首先探讨西边界流。接着上次的话题，黑潮和湾流变慢了吗？我们使用卫星高度计实测数据进行分析计算。

数据读取

首先要下载高度计再分析产品，这里我下载了欧洲cmems数据中心的高度计产品，下载地址是：

第一步制作一个文件列表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import os
from pathlib import Path

# 定义根目录
root_dir = Path("..", "dataset-duacs-rep-global-merged-allsat-phy-l4")

# 初始化一个空列表来存储所有文件路径
all_file_paths = []

# 循环遍历年份
for year in range(1993, 2019):
    # 循环遍历月份
    for month in range(1, 13):
        # 格式化月份，确保它总是两位数
        month_str = str(month).zfill(2)
        # 创建月份目录的路径
        month_dir = root_dir / str(year) / month_str
        
        # 检查目录是否存在
        if month_dir.exists():
            # 循环遍历月份目录中的文件
            for day_file in month_dir.iterdir():
                # 只考虑 .nc（NetCDF）文件
                if day_file.suffix == '.nc':
                    # 将完整文件路径添加到列表中
                    all_file_paths.append(day_file)

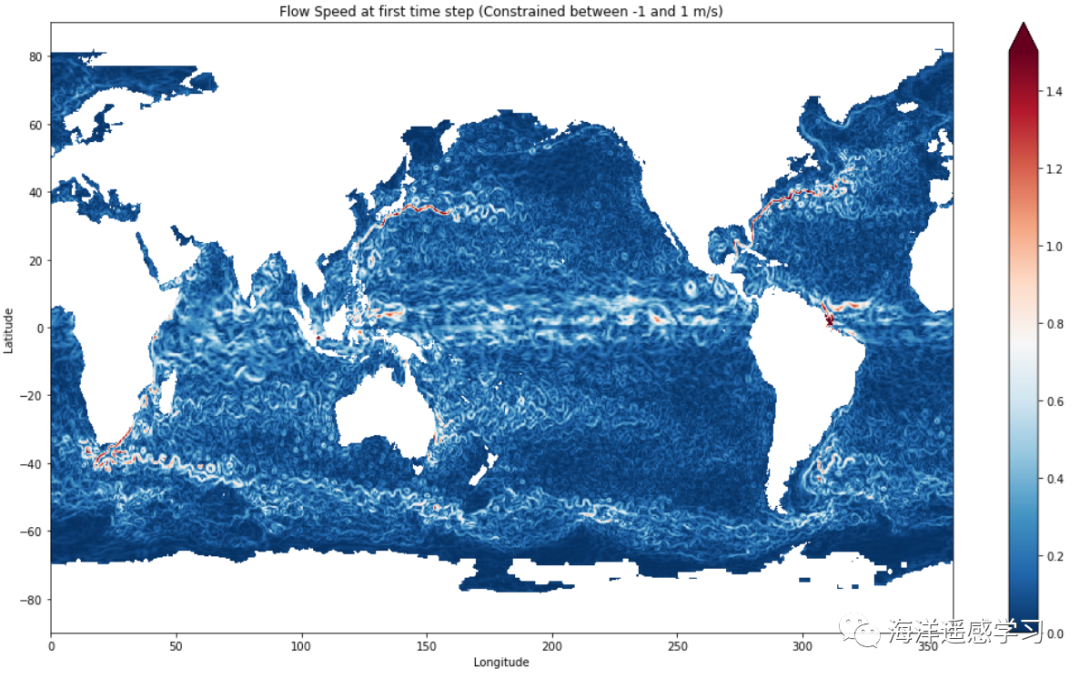
计算流速

初步观察利用高度计进行的全球流场分布，我们可以清楚地识别出主要的海洋流系统。这些包括南极绕极流、西边界流、赤道流等，以及众多大小不一的中尺度涡旋。这些观测结果生动地展示了海洋永无休止的旋转和流动。这些动态的海洋模式不仅是地球气候系统的重要组成部分，也对海洋生物的分布和迁移产生深远影响。通过细致分析这些流场分布，我们可以更深入地理解海洋动力学的复杂性和它们在全球环境中的作用。

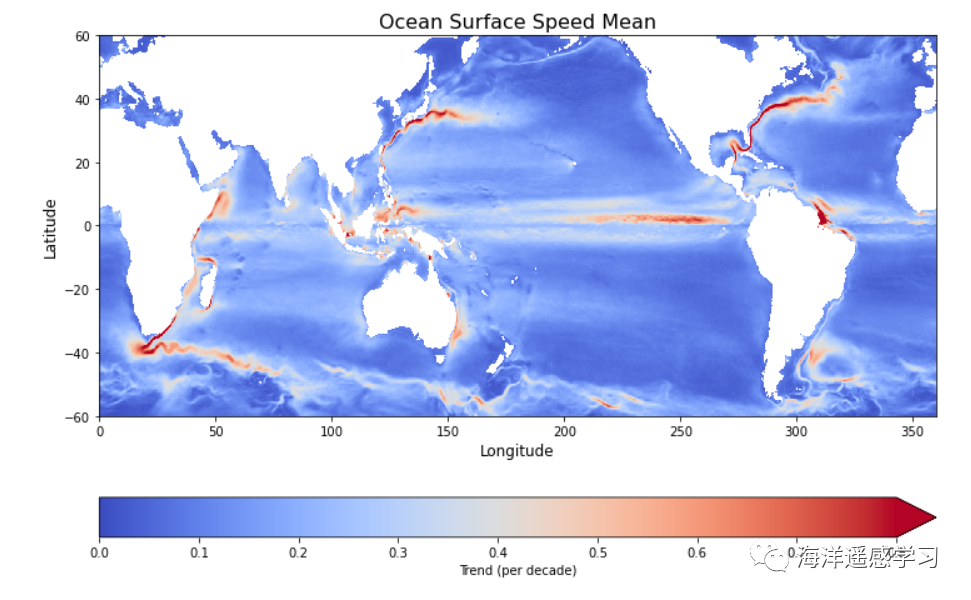
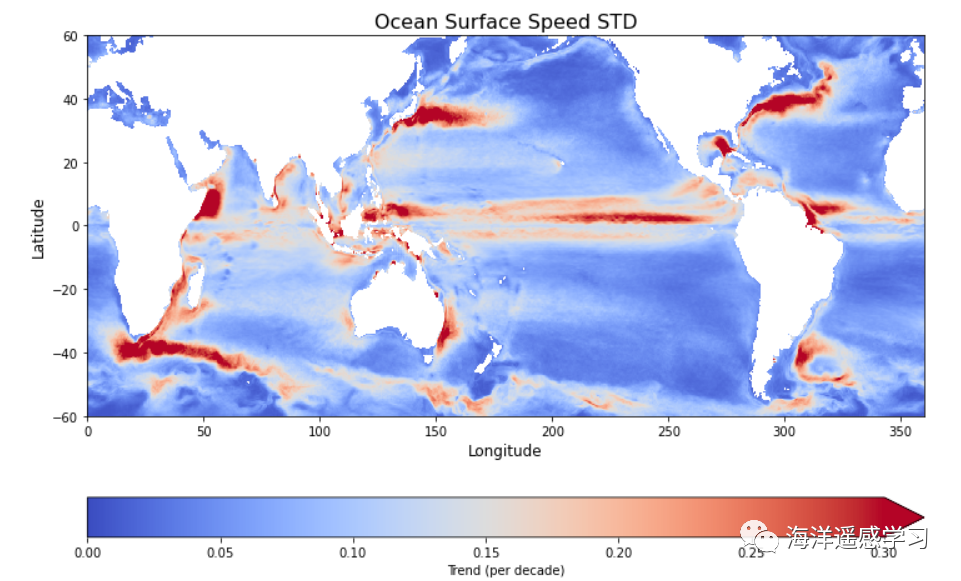
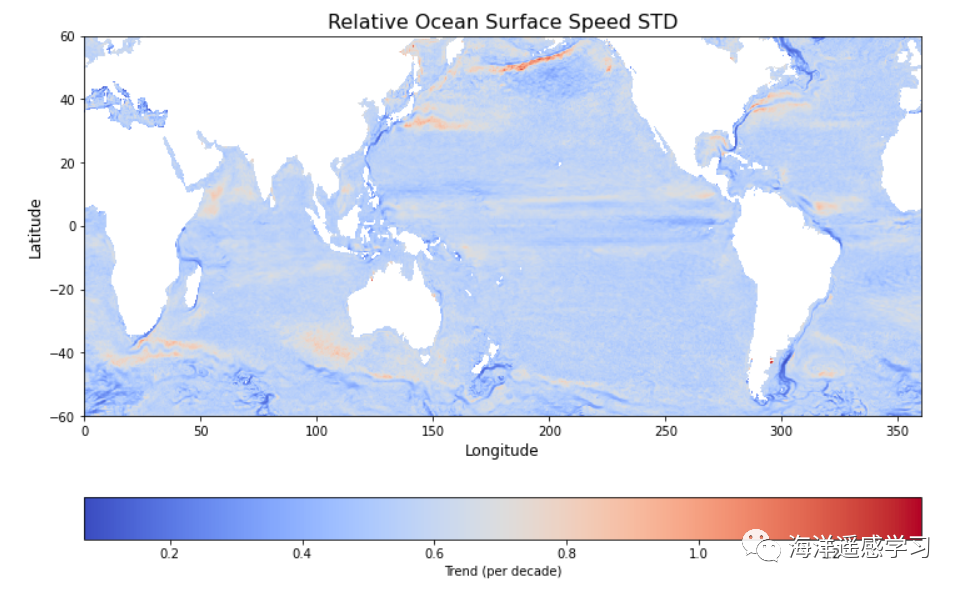
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
# Load the NetCDF file
file_path = all_file_paths[0]  # Get the first file path as a string
ds = xr.open_dataset(file_path)

# Extract the 'ugos' variable
ugos_data = ds['ugos']
# Extract the 'vgos' variable
vgos_data = ds['vgos']

# Calculate the magnitude of the velocity (flow speed) for the first time step
flow_speed = np.sqrt(ugos_data.isel(time=0)**2 + vgos_data.isel(time=0)**2)

# Plot the flow speed with constrained velocity range between -1 and 1 m/s
plt.figure(figsize=(18, 10))
flow_speed.plot(cmap='RdBu_r', vmin=-0, vmax=1.5)
plt.title('Flow Speed at first time step (Constrained between -1 and 1 m/s)')
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.show()

# 计算时间平均
time_mean_speed = speed_data_3d.mean(dim='time')

# 创建一个更大的图形
fig, ax = plt.subplots(figsize=(12, 8))

# 使用 xarray 的绘图功能，并设置数据范围为 ±0.2
plot = time_mean_speed.plot(ax=ax, cmap='coolwarm', 
                            cbar_kwargs={'label': 'Trend (per decade)', 'orientation': 'horizontal'},
                            vmin=-0.0, vmax=0.8)

# 添加标题和标签
plt.title('Ocean Surface Speed Mean', fontsize=16)
ax.set_xlabel('Longitude', fontsize=12)
ax.set_ylabel('Latitude', fontsize=12)

# 显示图形
plt.show()

# 计算时间标准差
time_std_speed = speed_data_3d.std(dim='time')

# 创建一个更大的图形
fig, ax = plt.subplots(figsize=(12, 8))

# 使用 xarray 的绘图功能，并设置数据范围为 ±0.2
plot = time_std_speed.plot(ax=ax, cmap='coolwarm', 
                            cbar_kwargs={'label': 'Trend (per decade)', 'orientation': 'horizontal'},
                            vmin=-0.0, vmax=0.3)

# 添加标题和标签
plt.title('Ocean Surface Speed STD', fontsize=16)
ax.set_xlabel('Longitude', fontsize=12)
ax.set_ylabel('Latitude', fontsize=12)

# 显示图形
plt.show()

# 计算相对时间标准差
relative_std_speed = time_std_speed / time_mean_speed


# 创建一个更大的图形
fig, ax = plt.subplots(figsize=(12, 8))

# 使用 xarray 的绘图功能，并设置数据范围为 ±0.2
plot = relative_std_speed.plot(ax=ax, cmap='coolwarm', 
                            cbar_kwargs={'label': 'Trend (per decade)', 'orientation': 'horizontal'}
                            )

# 添加标题和标签
plt.title('Ocean Surface Speed STD', fontsize=16)
ax.set_xlabel('Longitude', fontsize=12)
ax.set_ylabel('Latitude', fontsize=12)

# 显示图形
plt.show()




尽管高度计的观测揭示了多种海洋流系统和动态模式，但在今天的讨论中，我们将专注于西边界流的长期变化及其时空特征。考虑到数据量巨大，我们的代码中采取了特定的策略来优化数据处理流程。例如，通过设置for file_path in all_file_paths[::100]:，我们将每隔100天读取一次数据文件。这种方法旨在平衡数据的全面性与处理的可行性。读者可以根据自己的研究需求和资源限制，调整读取数据的间隔。这种灵活性使得我们的研究方法不仅适用于探索西边界流的长期趋势，也方便个性化地调整以适应不同的研究目标和数据集大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import xarray as xr
import numpy as np

# 初始化一个空的列表用于存储速度数据
speed_data = []

# 定义感兴趣的区域（纬度和经度的范围）
lat_min, lat_max = -60.0, 60.0
lon_min, lon_max = 0, 360.0

# 循环遍历每一个文件
for file_path in all_file_paths[::100]:
    # 打开NetCDF数据集
    ds = xr.open_dataset(file_path)
    
    # 提取感兴趣的区域
    ds_subset = ds.sel(latitude=slice(lat_min, lat_max), longitude=slice(lon_min, lon_max))
    
    # 提取 ugos 和 vgos 数据，并取第一个时间步
    u_gos = ds_subset['ugos'].isel(time=0)
    v_gos = ds_subset['vgos'].isel(time=0)
    
    # 计算速度
    u_speed = np.sqrt(u_gos**2 + v_gos**2)
    
    # 将计算出的速度添加到列表中
    speed_data.append(u_speed)
    
# 将列表转换为xarray DataArray 对象，从而形成一个3维数组
speed_data_3d = xr.concat(speed_data, dim='time')

# 显示结果（或进行后续分析）
# print(speed_data_3d)

长期趋势计算

首先，我们确定了数据集中时间、纬度和经度这三个维度的大小。这一步是为了确保我们精确地理解数据的结构，从而可以高效地处理和分析它。接着，我们初始化了一个数组，用于存储每个空间格点的趋势值。

紧接着，我们对每个格点进行了遍历。在每个格点，我们提取了随时间变化的速度数据，并运用线性回归来计算趋势。通过这种方法，我们能够量化每个格点上流速的变化趋势。更进一步，我们将这些趋势转换为每十年的变化率，这使得结果更加直观，也便于与历史数据或未来预测进行比较。

最后，我们利用xarray.DataArray将计算出的趋势值与其对应的空间坐标结合起来，形成一个新的数据结构，这使得数据更易于操作和分析。通过这样的数据处理和分析，我们能够更深入地理解西边界流随时间的变化，为研究全球气候变化及其对海洋环境的影响提供了宝贵的洞见。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 获取时间坐标信息，并转换为Pandas的TimedeltaIndex，以天为单位
time_coords = speed_data_3d.coords['time']
days = (time_coords - time_coords[0]).dt.days

# 获取时间维度的长度和空间维度的大小
n_time = speed_data_3d.shape[0]
n_lat = speed_data_3d.shape[1]
n_lon = speed_data_3d.shape[2]

# 初始化一个数组来存储每个格点的趋势
trend_array = np.zeros((n_lat, n_lon))

# 循环遍历每个格点
for i in range(n_lat):
    for j in range(n_lon):
        # 提取该格点的时间序列
        time_series = speed_data_3d[:, i, j].values  # 使用 .values 将xarray.DataArray转换为NumPy数组
        
        # 使用线性回归计算趋势
        slope, intercept = np.polyfit(days, time_series, 1)
        
        # 将趋势转换为每十年的量级（1年 = 365.25天）
        trend_per_decade = slope * 365.25 * 10
        
        # 存储趋势
        trend_array[i, j] = trend_per_decade

# 创建带有时间和空间坐标的趋势DataArray
trend_dataarray = xr.DataArray(
    trend_array,
    coords={
        "latitude": speed_data_3d.coords["latitude"],
        "longitude": speed_data_3d.coords["longitude"]
    },
    dims=["latitude", "longitude"]
)

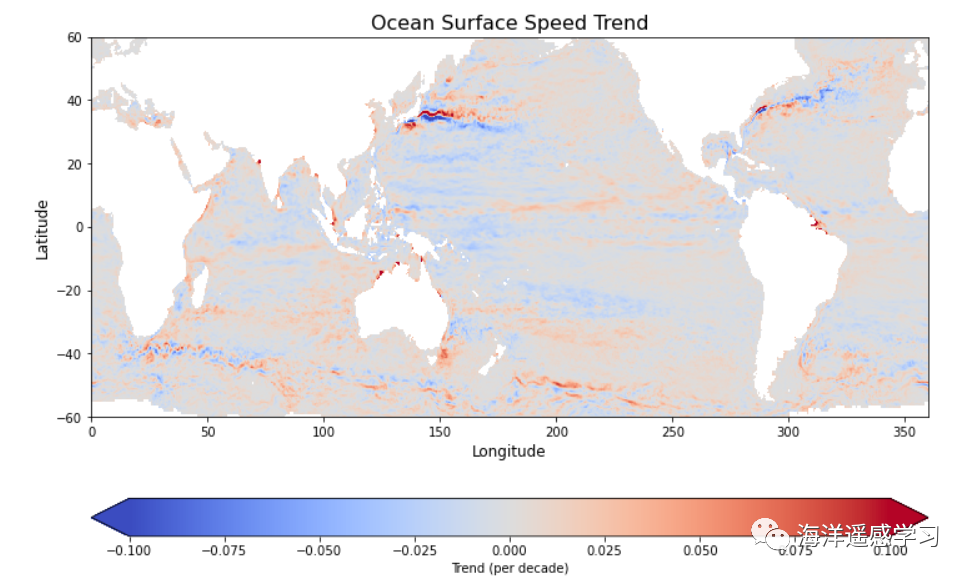
绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import matplotlib.pyplot as plt

# 创建一个更大的图形
fig, ax = plt.subplots(figsize=(12, 8))

# 使用 xarray 的绘图功能，并设置数据范围为 ±0.2
plot = trend_dataarray.plot(ax=ax, cmap='coolwarm',
                            cbar_kwargs={'label': 'Trend (per decade)', 'orientation': 'horizontal'},
                            vmin=-0.1, vmax=0.1)

# 添加标题和标签
plt.title('Ocean Surface Speed Trend', fontsize=16)
ax.set_xlabel('Longitude', fontsize=12)
ax.set_ylabel('Latitude', fontsize=12)

# 显示图形
plt.show()

这幅地图展示了全球海洋表面流速的趋势分布，色标从蓝色到红色代表了流速趋势的变化范围，蓝色代表速度减缓（负趋势），而红色代表速度加快（正趋势）。可以观察到，特定区域如西边界流域显示出明显变化趋势，但呈现出条纹状，意味着这些区域的海流速度在过去十年既有有增加的趋势，又有下降的趋势。这背后的机制可能是由于局部海洋环流的变化或长期的气候模式变动所导致。

我们把黑潮和湾流区进行放大观察：

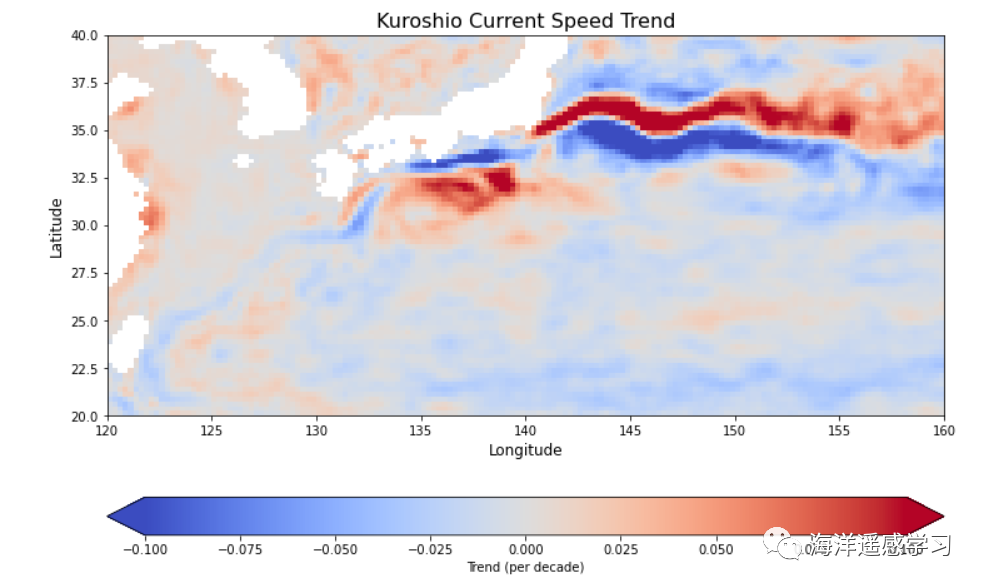
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt

# 选择黑潮区域的数据
kuroshio_trend = trend_dataarray.sel(latitude=slice(20, 40), longitude=slice(120, 160))

# 创建一个更大的图形
fig, ax = plt.subplots(figsize=(12, 8))

# 使用 xarray 的绘图功能，并设置数据范围为 ±0.1
plot = kuroshio_trend.plot(ax=ax, cmap='coolwarm',
                           cbar_kwargs={'label': 'Trend (per decade)', 'orientation': 'horizontal'},
                           vmin=-0.1, vmax=0.1)

# 添加标题和标签
plt.title('Kuroshio Current Speed Trend', fontsize=16)
ax.set_xlabel('Longitude', fontsize=12)
ax.set_ylabel('Latitude', fontsize=12)

# 显示图形
plt.show()

我们可以对黑潮及其延伸体的长期变化进行一些具体分析。黑潮作为西太平洋的一个主要海流，其主轴的流速趋势在这幅图中没有显示出明显的增强或减弱的迹象，这表明在观测期间，黑潮主轴的强度保持相对稳定。

然而，值得注意的是，在黑潮延伸体的区域，地图展示了一种流轴北移的现象。具体来说，这意味着在黑潮南侧的海域流速变慢（如图中蓝色区域所示），而北侧的流速有所增加（相应的红色区域）。这种变化可能指示了海流的某种空间重组，它可能与多种海洋和气候因素有关，如北太平洋年代际振荡（PDO）、黑潮大弯曲事件和全球变暖，以及局部风场的变化、海水温度梯度的变化，以及其他影响海流结构和强度的因素。

总体上，地图上的色彩分布似乎显示了一种对称守恒的格局，即南侧减慢的流速和北侧加快的流速在数量上相互抵消。这种对称性可能反映了黑潮系统内部动力学的一个重要特性，即在某些自然变化或外部强迫下，系统倾向于通过调整其流速分布来维持能量的平衡。这些观测结果对于理解区域海洋动力学的变化具有重要意义，并可能为预测黑潮以及其延伸体在未来气候变化情景下的响应提供线索。

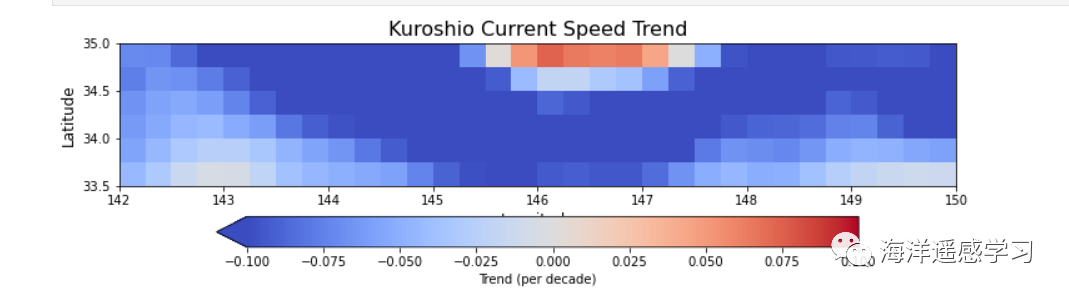
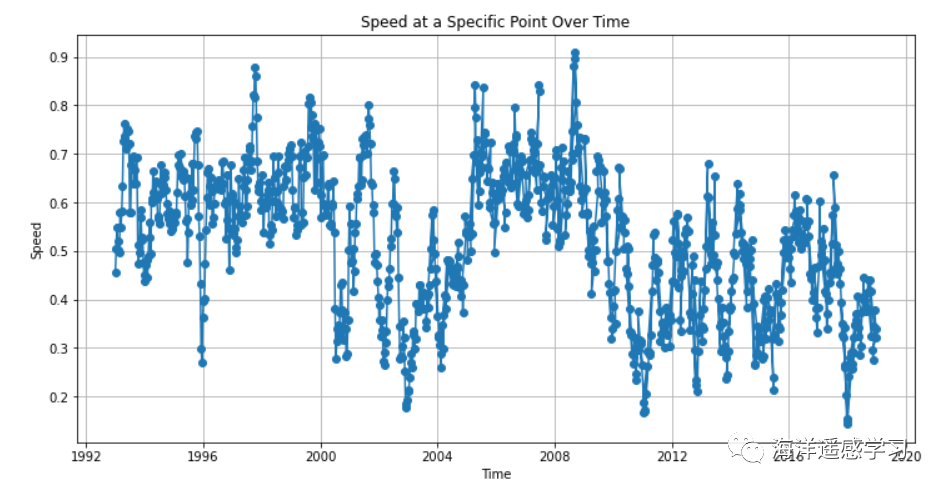
观察空间分布上表现出减速趋势的海域，并对其时间序列进行分析，这是理解海洋流速变化的重要环节。结果显示这些海域的流速确实在减慢，且这一减慢的趋势是非线性的，变化过程中还伴随着波动。非线性的趋势和中间的波动意味着这些海域的流速变化并非单一方向上的简单增减，而是包含了多个时间尺度上的复杂动力过程。例如，可能存在一个长期的减速趋势，但在这个趋势中叠加了短期的加速和减速周期。这些波动可能是由季节性因素、气候事件如厄尔尼诺或拉尼娜现象，甚至是更长期的气候循环模式所导致的。

要深入理解这些非线性变化，可能需要应用高级的统计方法或时间序列分析工具，例如小波分析或傅立叶变换，以识别和分离出不同时间尺度上的变化成分。此外，与气候模型输出和长期观测数据相结合的方法可以帮助揭示造成这些变化的潜在机制，并预测未来的变化趋势。这对于预测海洋环流如何影响全球气候系统以及海洋生态系统至关重要。

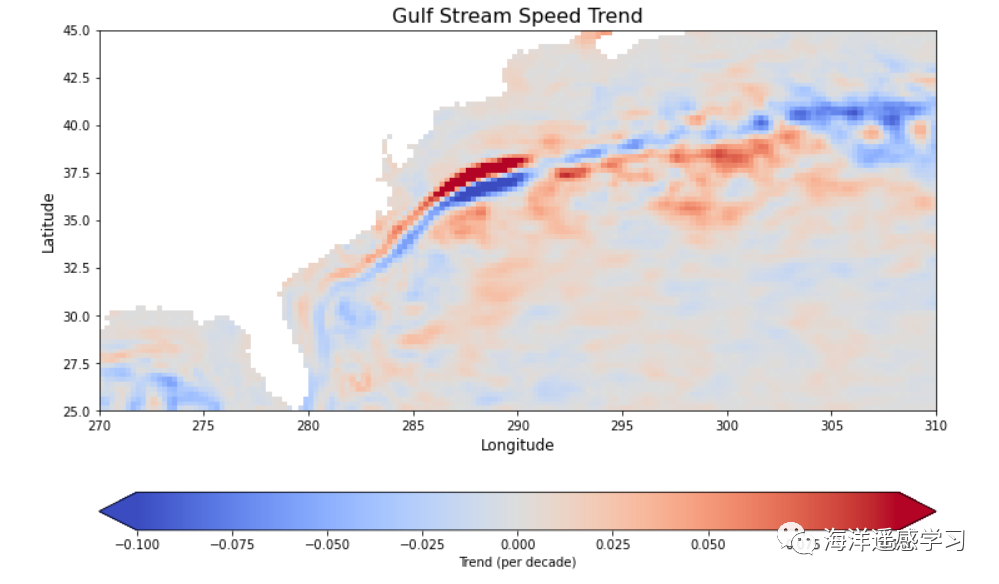
湾流也呈现出类似的特征。湾流作为北大西洋的一个主要暖流，对调节北半球的气候起着至关重要的作用。我们看到湾流也显示出北移现象，这可能意味着流速在南侧减慢而北侧增快。这样的变化可能与大尺度气候模式如北大西洋涛动（NAO）或全球变暖背景下的海水温度变化有关。湾流的这种行为可能会导致能量分布的重新配置，并可能对北大西洋的海洋生态系统和欧洲的气候产生影响。

问题探讨

  • 西边界流是全球最稳定的洋流，为什么东向流动的延伸体会向北移动？
  • 具体的机制是什么？

西边界流的稳定性和其东向流动的延伸体北移现象确实是一个引人入胜的研究话题。西边界流，如北太平洋的黑潮和北大西洋的湾流，通常是强大而稳定的，这主要是由于它们在特定的海洋盆地边缘受到地形的引导和科里奥利力的影响。东向流动的延伸体向北移动可能与多种因素有关，包括但不限于海水温度变化、风应力的变化、气候变化导致的大尺度气候模式的漂移。

如解决上面的问题，我相信这将是一篇NS级别的文章吧，希望有兴趣的兄弟们可以试一试，也可以联系我一起合作。

下节预告

  • 卫星高度计探测Rossby wave