0%

人工智能海底地形反演(2)-重力数据处理

发表于 更新于 阅读次数： Valine：

上节说到人工智能水深反演的单波束质控，这一步骤十分重要，最后的结论表明质控后的反演结果精度可提高三倍。单波束在AI反演水深的角色是label，训练数据集则是重力数据，本节介绍从卫星测高到重力异常的反演方法和数据处理。

需具备的编程知识点

  • GMT
  • Python
  • Jupyter Lab
  • Fortran（测高重力反演源码）

卫星测高数据反演重力异常

在我们的AI水深反演中，重力异常以及相关的衍生产品如垂直重力梯度、垂线偏差等是主要的训练数据集合。通常这些产品可以从Sandwell或Anderson（DTU）学术网站下载。Sandwell和DTU产品被广泛使用，其认可度高，可以拿来直接使用，因此我们无需增加自己的重力反演计算工作。

这里我们选择Sandwell的产品，因为它提供了上述所有产品。

下载地址：https://topex.ucsd.edu/pub/global_grav_1min/

如果读者希望自己重复一遍重力反演过程，也是可以的，这可以提高自己对测高重力反演的认识，我们简单概述测高重力反演：

海水和海底玄武岩的密度差异导致了微弱的重力异常信号，这种重力异常信号将海水拽向海山处，进而使海面高度产生起伏（也称大地水准面）。测高反演重力的基本原理即利用这种相关性，它的反演方法在上世纪90年代左右就有了，目前已成熟稳定。方法大致分两类，一类是基于大地水准面起伏(SSH方法)，一种是基于垂线偏差（Sea surface slope，SSS方法）。SSH方法通过逆斯托克斯公式和最小二乘配置构建了重力异常和水准面起伏的关系，SSS方法通过逆Vening–Meinesz公式和Laplace方程构建了垂涎偏差和重力异常的关系，这两种方法均基于海面高度信息和重力信号的物理关系。尽管这些公式较长，难以完全理解，不过台湾交通大学Huang教授共享了一套简便的程序代码，并且在国科大授课期间分发给学员学习使用，从事本领域的读者应该容易得到这些源代码。如果您没有这些源码，也可回复本文索取，或者扫描文末二维码加入AI反演大赛微信群索取。

总而言之，重力反演并不是AI水深的重点和难点。这里我们暂时省略这部分工作，而是使用Sandwell公布的重力产品。

等一段时间，小编将邀请国内重力大咖讲解AI反演重力，据说效果可好了。

重力数据预处理

因为下载的模型是全球模型，首先使用pygmt提取研究区域重力网格数据，分别是重力异常、垂直重力梯度、东西垂线偏差、南北垂线偏差。为保持后面的边界插值准备，这里的region略大一点。为避免网格不对应，这里还特意重新网格化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
free = pygmt.grdcut(grid="../GeoModel/Free_Air_Gravity_Anomalies/Free_Air_Gravity_Anomalies.nc", region="-15.5/5.5/-4.5/4.5")
free.to_netcdf("free2.grd")

vgg = pygmt.grdcut(grid="../GeoModel/Vertical_Gravity_Gradient/Vertical_Gravity_Gradient.nc", region="-15.5/5.5/-4.5/4.5")
vgg_1m=pygmt.grd2xyz(grid=vgg)
pygmt.surface(region=reg, spacing="1m",outgrid="vgg.grd",data=vgg_1m)


nvd = pygmt.grdcut(grid="../data/north_32.1.nc", region="-15.5/5.5/-4.5/4.5")
nvd_1m = pygmt.grdsample(grid=nvd, spacing="1m")
nvd_1m=pygmt.grd2xyz(grid=nvd)
pygmt.surface(region=reg, spacing="1m",outgrid="nvd.grd",data=nvd_1m)

evd = pygmt.grdcut(grid="../data/east_32.1.nc", region="-15.5/5.5/-4.5/4.5")
evd_1m=pygmt.grd2xyz(grid=evd)
pygmt.surface(region=reg, spacing="1m",outgrid="evd.grd",data=evd_1m)

重力异常、VGG和东西、南北垂线偏差如下图，绘图代码略，这里使用的调色板是polar：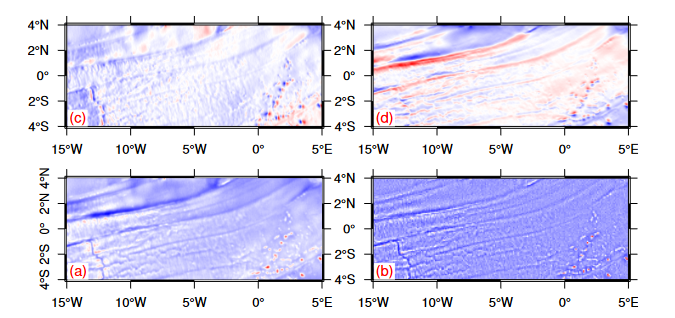

短波重力计算

重力信号中实际和地形相关的是短波分量，传统的GGM方法就使用了短波重力来反演水深，短波重力可以通过布格板公式计算，这里有一个最优密度差的计算，需要通过迭代确定。通过计算，我们发现几内亚湾的最优密度差是1。

其思路是：提取实测单波束点位的重力异常，使用布格板公式计算离散点的短波重力，使用重力异常减去短波重力得到离散点的长波重力，对长波重力做网格化，使用网格化的重力异常减去长波重力，得到网格化的短波重力。

python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
control_depth_free=pygmt.grdtrack(points=control.values,grid="free2.grd",no_skip=True)
y_train1 = control_depth_free.values[:,0:3] # lon lat depth
x_train1 = control_depth_free.values[:,3] # gravity
x_train1 = np.reshape(x_train1, (len(x_train1), 1))

x_lat = np.reshape(y_train1[:, 1], (len(y_train1[:, 1]), 1))
x_lon = np.reshape(y_train1[:, 0], (len(y_train1[:, 0]), 1))

rou=1.0
d=-8000
control_short=(y_train1[:,2]-d)*2*3.1415*6.67259*(10**-8)*rou*100000 # short wavelength gravity ano
control_short = np.reshape(control_short, (len(control_short), 1))
control_long=x_train1-control_short
short=np.concatenate((y_train1[:,0:2],control_short),axis=1)
long=np.concatenate((y_train1[:,0:2],control_long),axis=1)
reg="-15.5/5.5/-4.5/4.5"

long_bmean = pygmt.blockmean(data=long, region=reg, spacing="1m")
pygmt.surface(region=reg, spacing="1m",outgrid="long.grd",data=long_bmean)
temp=pygmt.grd2xyz(grid="free2.grd")
temp_bmean = pygmt.blockmean(data=temp, region=reg, spacing="1m")
pygmt.surface(region=reg, spacing="1m",outgrid="free3.grd",data=temp_bmean)

long0 = xr.open_dataset("long.grd")
free0 = xr.open_dataset("free3.grd")
short0 = free0-long0
short0.to_netcdf("short.grd")

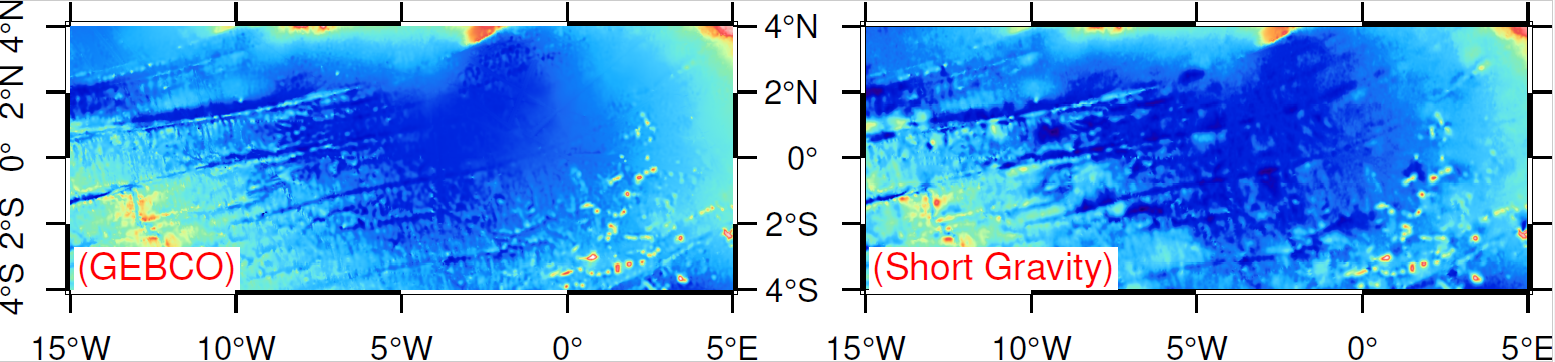
下图是短波重力和海底地形的对比效果，如果不标注名称，似乎看不出来差异，这也说明短波重力和海底地形的相关性太强了。在AI中加入短波重力，预计将大幅度提供反演精度。问题是AI能否由于GGM？希望在我们即将举办的AI算法大赛中有人使用AI打败GGM。

问题：地址模型磁异常、洋壳年龄、沉积层厚度等能否应用于AI水深？

小结

下节预告

  • AI训练前的数据预处理

AI水深反演大赛交流预热群

对AI水深反演和卫星测高重力有兴趣的伙伴可以扫码入群交流。