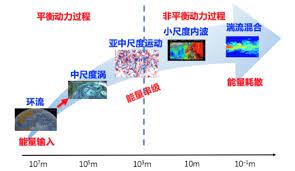
在地球旋转作用下,海洋表现出永恒的、自然的运动。海洋运动包含环流和波动,在时间和空间的不同尺度上具有一定的自然规律和特点,简单说中尺度海流为平衡的地转运动,可以输运物质能量,小尺度的波动是非地转非平衡运动,起到能量传播作用,不输运物质,波浪只做周期往复的椭圆运动。
当前的海洋观测手段主要是卫星观测、定点观测和漂流浮标观测,得到时间上高频(小时)和空间上高波数(亚中尺度)的全球海洋环流观测基本是不可能的,例如传统高度计分辨率的有效分辨率在100km,时间分辨率为1天。
当前波动(含内波)已经在它的领域得到了大量的独立研究,中尺度和大尺度的环流也在它的领域被大量的独立研究,而介于中尺度和小尺度之间的亚中尺度运动依旧是人类认识海洋的空白区之一。LLC4320的高分辨率允许我们使用它进行高频、高波数时空谱分析,得到亚中尺度谱形状特征,进而了解海洋动能的时空特征和注入、级串、耗散等过程。
本节,我们使用LLC4320云计算快速计算wavenumber-frequency谱(w-f谱),的得到三维的FFT结构,并分离海洋中的平衡和非平衡运动。
参考:https://github.com/pangeo-data/swot_adac_ogcms
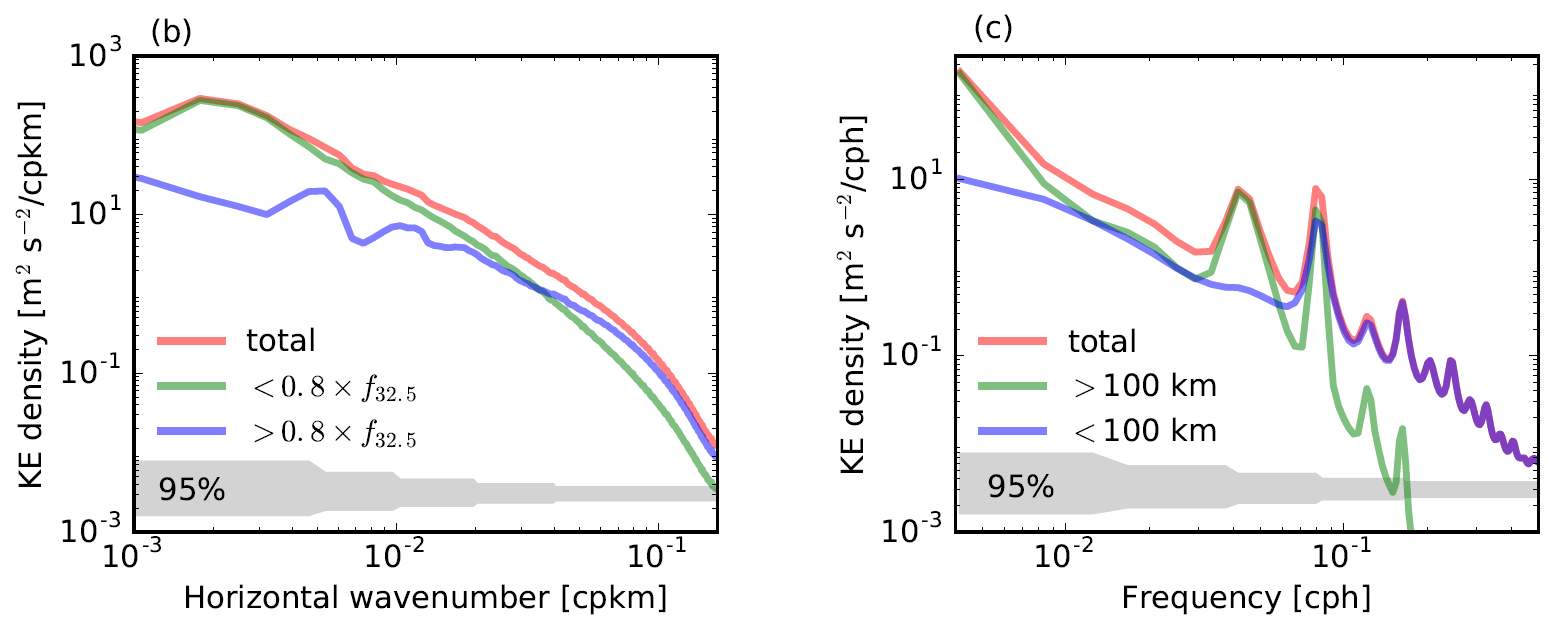
思路 气象海洋数据往往是三维或者更多维度结构,对于含有空间和时间的三维网格数据,可以计算每个网格点的时间FFT,也可以计算每个时刻的空间FFT。分开计算的效果往往是下面两张图,这样的谱表达是时空分割的,无法同时知道时间和空间尺度的内在关系:
w-f谱本质上是在时间和空间上先后做了FFT。那么把时间和空间都同时进行FFT,则可以得到物理海洋常见的三维w-f谱,其中两个坐标轴分别表示时间频率和空间波数,颜色表示能量密度大小。
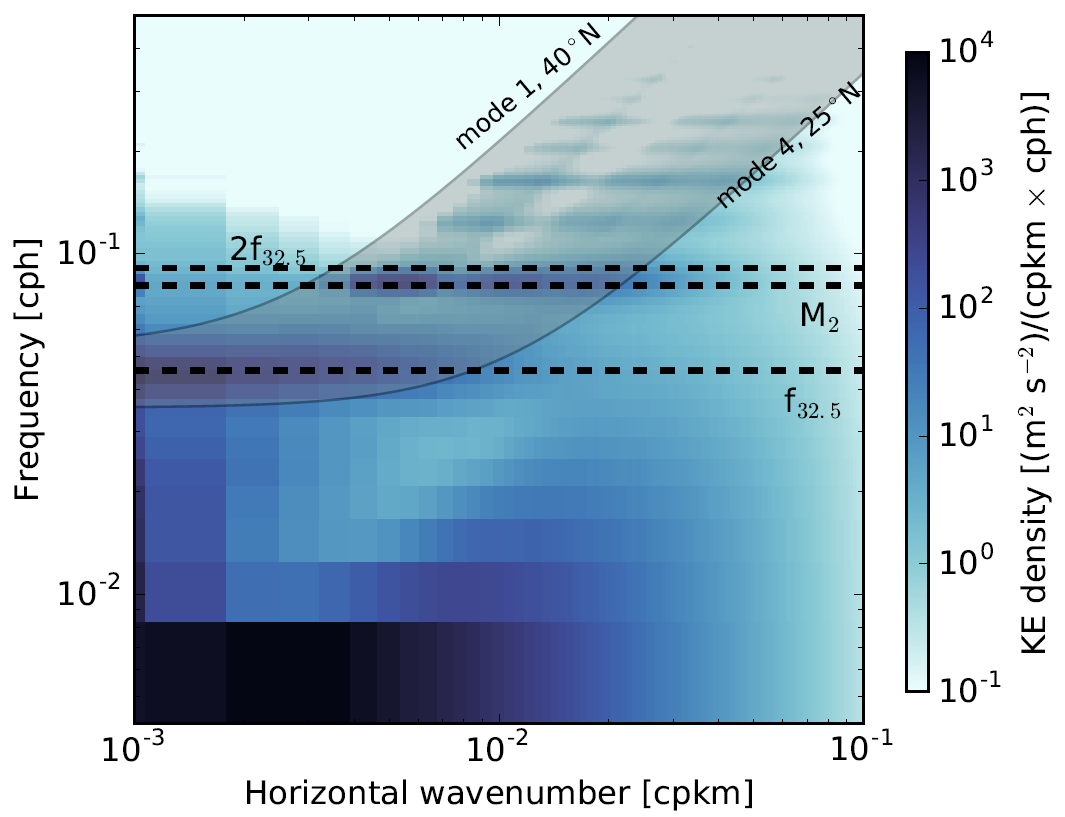
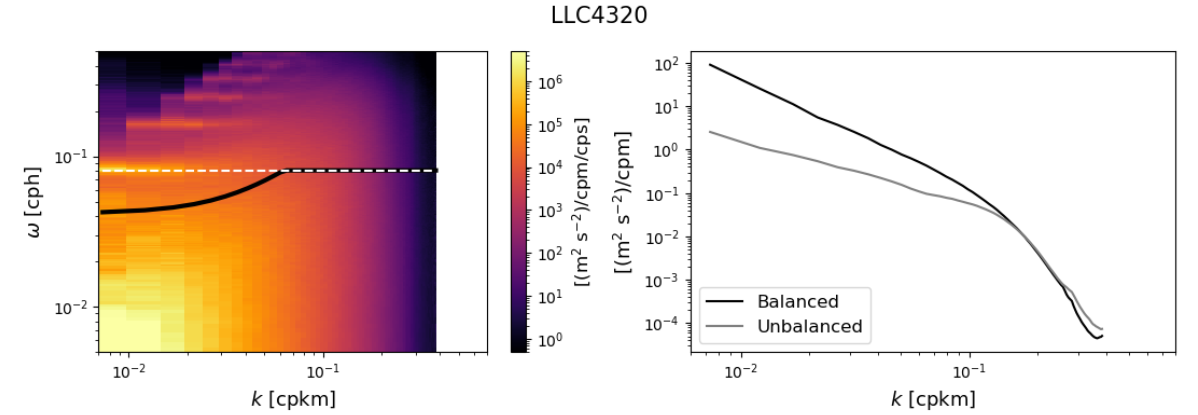
效果往往是下面的图,初看可能很混乱,我大致描述下它的含义。在时间尺度上海洋运动的周期性非常明显,在潮汐周期M2频率上会发现一条高能带,如果平行着Y轴做一条剖面线,则在M2有一个峰,f是科氏力参数,也表示地转频率或者惯性频率,和纬度有关系,它是区分平衡运动和非平衡运动的一个重要参数,图上的两条曲线是内波的不同模态,内波的第十模态(图上无此模态)往往也是区分平衡和非平衡运动的一个频率分界线。当前最新的研究成果表明,从海面观测信息中区分地转和非地转能量的参考正是惯性频率和内波模态的结合。
摘自:C. B. Rocha, S. T. Gille, T. K. Chereskin, and D. Menemenlis, “Seasonality of submesoscale dynamics in the Kuroshio Extension,” Geophysical Research Letters, vol. 43, no. 21, p. 11,304-11,311, 2016, doi: 10.1002/2016GL071349.
代码 下面使用云计算和LLC4320模式数据,介绍主要的计算步骤,由于代码略多,这里仅贴出关键部分,最后附完整代码(notebook)下载地址。
首先导入库(略) 云数据读取 同时导入LLC4320的表面流速UV,以及模式的网格文件。计算全球数据需要消耗太大的计算,这里我们选择美国西海岸的湾流区域为例进行分析,时间选择春季。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 from intake import open_catalog import xmitgcm.llcreader as llcreader cat = open _catalog("https://raw.githubusercontent.com/pangeo-data/pangeo-datastore/master/intake-catalogs/ocean/llc4320.yaml" ) u = cat.LLC4320_SSU .to _dask() v = cat.LLC4320_SSV .to _dask() ds = xr.merge([u , v ] ) ds = llcreader.llcmodel.faces_dataset_to_latlon(ds , metric_vector_pairs =[]) coords = cat.LLC4320_grid .to _dask() .reset_coords() coords = llcreader.llcmodel.faces_dataset_to_latlon(coords ) llcw0=ds.sel(time=slice('2012 -02 -01 ',' 2012 -04 -30 ')).isel(j=slice(9555 ,10198 -115 ),j_g=slice(9555 ,10198 -115 ), i=slice(15355 +170 ,15845 ),i_g=slice(15355 +170 ,15845 ))
载入网格信息,主要用于计算空间间隔:
1 2 3 4 5 6 7 dxC_sel = coords.dxC.isel(i_g=slice(15355 +170 ,15845 ), j=slice(9555 ,10198 -115 )) dyG_sel = coords.dyG.isel(i_g=slice(15355 +170 ,15845 ), j=slice(9555 ,10198 -115 )) dyC_sel = coords.dyC.isel(i=slice(15355 +170 ,15845 ), j_g=slice(9555 ,10198 -115 )) dxG_sel = coords.dxG.isel(i=slice(15355 +170 ,15845 ), j_g=slice(9555 ,10198 -115 )) XC_sel = coords.XC.isel(i=slice(15355 +170 ,15845 ), j=slice(9555 ,10198 -115 )) YC_sel = coords.YC.isel(i=slice(15355 +170 ,15845 ), j=slice(9555 ,10198 -115 )) dyG_sel= coords.dyG.isel(i_g=slice(15355 +170 ,15845 ), j=slice(9555 ,10198 -115 ))
合并:
1 2 llcw2 = xr.merge([llcw0, dxC_sel, dyC_sel, dxG_sel, dyG_sel,XC_sel, YC_sel,dyG_sel])
数据预处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 metrics = { ('X' ,): ['dxC' , 'dxG' ], # X distances ('Y' ,): ['dyC' , 'dyG' ], # Y distances # ('Z' ,): ['drC' ], # Z distances # ('X' , 'Y' ): ['rA' , 'rAs' , 'rAw' ] # Areas } gridllc = Grid(llcw2, periodic=[], coords={ # 'Z' :{'center' :'k' ,'outer' :'k_p1' }, 'Y' :{'center' :'j' ,'left' :'j_g' }, 'X' :{'center' :'i' ,'left' :'i_g' }}, metrics=metrics )
在海洋模式中不同变量彼此偏移,并位于不同的位置,例如LLC4320关于位置有许多的坐标轴,i,i_g,j,j_g等均表示这类意思。这些网格为xarray数据模型操作带来了两难境地,这意味着它们不能使用一致的坐标来表示,xgcm 的一个目标是通过插值进行坐标统一。
U的坐标轴原本是(j,i_g),下面将转换为(j,i):
1 gridllc.interp(llcw2.U,'X' ,boundary ='extend' ) # 坐标轴的变换
FFT操作的对象是距离单位,而不是网格单位,因此需要把网格近似转换为距离,并得到重组的结构化xarray,便于后续的FFT输入。
1 2 3 4 5 6 7 8 9 10 11 12 with ProgressBar(): U_llc = xr.DataArray(llcw2.U, dims=['time' ,'YC' ,'XC' ], coords={'time' :np .arange(len(llcw2.U.time))*3600 , 'YC' :np .arange(0,Ny1*dy1,dy1), 'XC' :np .arange(0,Nx1*dx1,dx1)} ).chunk({'time' : 100 ,'YC' :- 1 ,'XC' :- 1 }) V_llc = xr.DataArray(llcw2.U, dims=['time' ,'YC' ,'XC' ], coords={'time' :np .arange(len(llcw2.U.time))*3600 , 'YC' :np .arange(0,Ny1*dy1,dy1), 'XC' :np .arange(0,Nx1*dx1,dx1)} ).chunk({'time' : 100 ,'YC' :- 1 ,'XC' :- 1 })
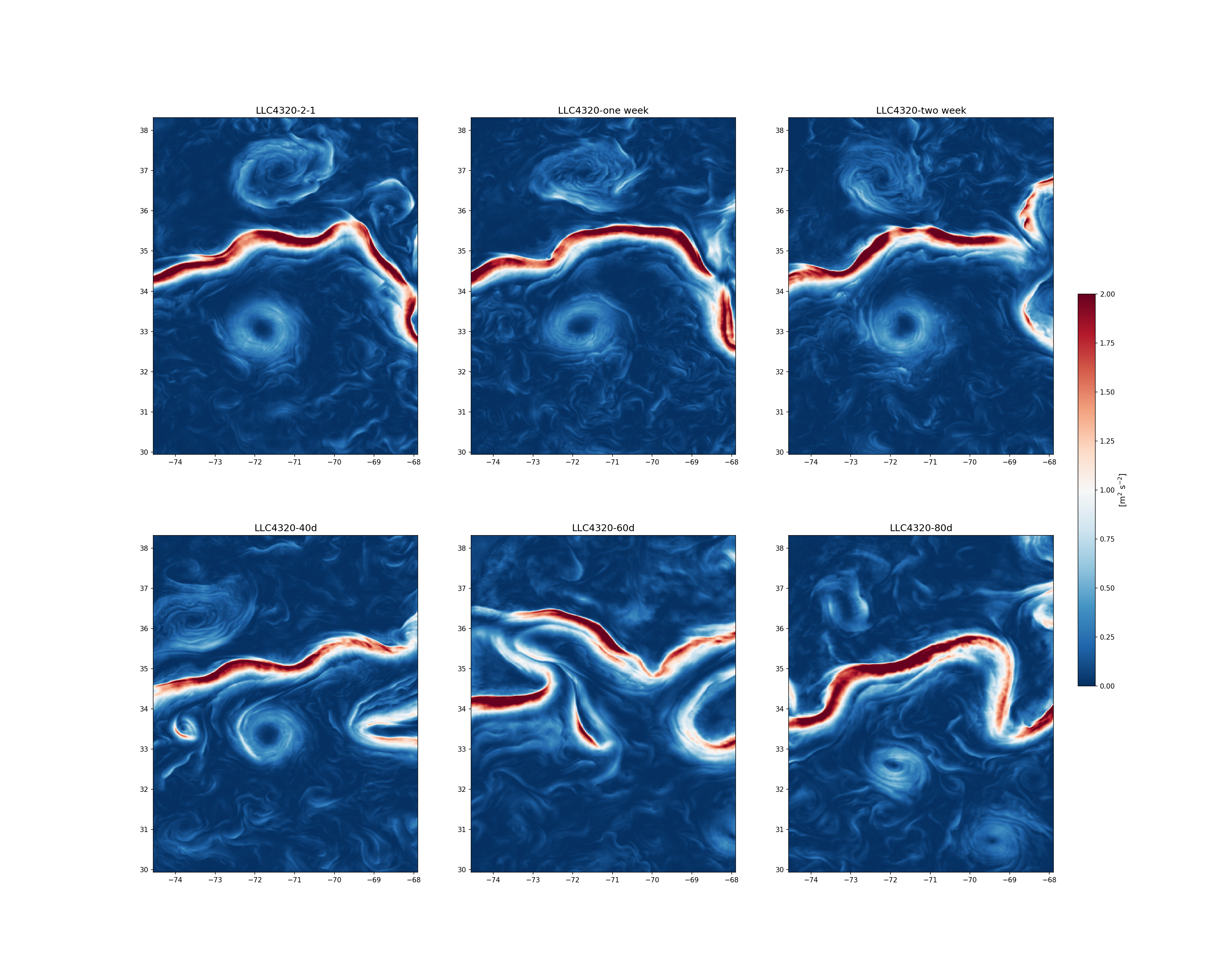
时空 下面我们先展示湾流地区精美的KE时空结构变化,(文末可下载全部代码)。那么怎么挖掘里面的科学信息呢?谱分析或许是很好的方法之一。
谱分析 下面是最核心的FFT计算,可以看到它的本质是连续在空间和时间上进行FFT,注意dim表示FFT处理的时空维度。得到谱信息后,还需要要做各项同性的规则化处理(代码略)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 %%time # FFT. 先进行空间的,在进行时间的,最后得到的两个都有 Fu_llc = xrft.fft(xrft.fft(U_llc.fillna(0. ), dim=['YC' ,'XC' ], window ='hann' , detrend='constant' , true_phase=True , true_amplitude=True ).chunk({'time' :-1 ,'freq_YC' :200 ,'freq_XC' :200 }), dim=['time' ], window ='hann' , detrend='constant' , true_phase=True , true_amplitude=True ) Fu_lls = Fu_llc.isel(freq_time=slice (len(Fu_llc.freq_time)//2 ,None )) * 2 Fv_llc = xrft.fft(xrft.fft(V_llc.fillna(0. ), dim=['YC' ,'XC' ], window ='hann' , detrend='constant' , true_phase=True , true_amplitude=True ).chunk({'time' :-1 ,'freq_YC' :200 ,'freq_XC' :200 }), dim=['time' ], window ='hann' , detrend='constant' , true_phase=True , true_amplitude=True ) Fv_llc = Fv_llc.isel(freq_time=slice (len(Fv_llc.freq_time)//2 ,None )) * 2
绘图 首先设计一个plot函数(代码略),然后调用绘图:
1 2 3 4 5 6 7 8 9 10 enatlf = xr.DataArray(xr.apply_ufunc(gsw.f, llcw2.YC, dask ='parallelized' ).data, dims=['YC' ,'XC' ], coords={'YC' :U_llc.YC,'XC' :U_llc.XC}) omega = np.sqrt(((enatlf.isel(YC =0))**2).mean() + cs**2 *(isoFu_llc.freq_r.isel(freq_r =slice(1,None))*2*np.pi)**2 )/2/np.pi omega = xr.DataArray(np.minimum(omega, m2/3600), dims ='freq_r' , coords={'freq_r' :isoFu_llc.freq_r.isel(freq_r =slice(1,None))} ) plot(.5*(isoFu_llc + isoFv_llc), omega, enatlf,title =r"LLC4320")
这样我们就得到了物理海洋最常用的w-f谱分析图,同时还利用能量积分方法分离了平衡和非平衡运动。关于里面的科学性问题,已有大量论文进行了解读,本文仅技术性描述计算过程。
小结
下结预告
物理海洋是不是有点难?休息休息
海洋测绘的AI应用,以海底地形为例